Newton’s Law of Gravitation: The Force That Governs the Universe
Estimated reading time: 10 minutes
Gravity is one of the fundamental forces of nature that governs the motion of celestial bodies, keeps planets in their orbits, and determines the weight of objects on Earth. Sir Isaac Newton formulated the Universal Law of Gravitation in the 17th century laying the foundation for classical mechanics. Therefore, gravity is essential in understanding planetary motion, satellite dynamics, and even the formation of galaxies. In this article, we will explore the concept of gravity, central forces, and the mathematical framework that describes this invisible yet powerful force in detail.
Gravity may put the planets into motion, but without the divine Power, it could never put them into such a circulating motion as they have about the Sun; and therefore, for this as well as other reasons, I am compelled to ascribe the frame of this System to an intelligent Agent.
-Isaac Newton
What are Central Forces?
A central force is a force that always acts along the line joining an object to a fixed point. Additionally, its magnitude depends only on the distance between the object and that point. Mathematically, a force ![]() is called a central force if it satisfies the condition:
is called a central force if it satisfies the condition:
![]()
where:
 is a function of distance
is a function of distance  ,
,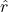 is the unit vector pointing radially outward from the central point.
is the unit vector pointing radially outward from the central point.
Gravitational Force as a Central Force
Gravitational force is a classic example of a central force because it always acts along the line joining two masses and depends only on the distance between them. Consequently, this property is essential in understanding planetary motion, satellite dynamics, and orbital mechanics, all of which follow from Kepler’s Laws and Newton’s Law of Gravity.
For instance, some other examples of central forces include:
- Electrostatic forces between charged particles
- Magnetic forces under specific conditions
Key Properties of Central Forces in Gravity
- Radial Dependence: The magnitude of gravitational force depends only on the distance
 , meaning it follows the form
, meaning it follows the form 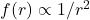 .
. - Conservative Nature: Gravitational force is a conservative force, meaning the work done in moving a mass in a closed path around another mass is zero.
- Angular Momentum Conservation: Moreover, in a central force field like gravity, the angular momentum of an orbiting body is conserved:
![Rendered by QuickLaTeX.com \[\mathbf{L} = \mathbf{r} \times \mathbf{p} = \text{constant}\]](https://entechonline.com/wp-content/ql-cache/quicklatex.com-deeecff268ff1bc5796f40f9733e485f_l3.png)
Subsequently, this leads directly to Kepler’s Second Law, which states that a planet sweeps out equal areas in equal time intervals. - Origin of Orbital Motion: Since gravitational force is central, it does not exert a torque about the central mass (e.g., the Sun in planetary motion). This is why planets move in stable elliptical orbits according to Kepler’s First Law.
Newton’s Universal Law of Gravitation
Newton’s Universal Law of Gravitation states that every mass in the universe attracts every other mass with a force that is:
- Directly proportional to the product of their masses.
- Inversely proportional to the square of the distance between their centers.
Furthermore, this can be expressed mathematically as:
![]()
where:
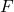 is the gravitational force between two objects,
is the gravitational force between two objects,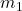 and
and 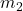 are the masses of the objects,
are the masses of the objects, is the distance between their centers,
is the distance between their centers,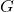 is the gravitational constant.
is the gravitational constant.
This law explains why planets orbit the Sun and why objects fall towards the Earth. Hence, it forms the foundation for celestial mechanics and space exploration.
The Gravitational Constant (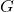 )
)
The gravitational constant, ![]() , is a fundamental physical constant with a value of approximately:
, is a fundamental physical constant with a value of approximately:
![]()
Since this constant determines the strength of gravitational attraction in the universe, it is widely used in Astrophysics. In other words, its small value indicates that gravity is the weakest of the four fundamental forces. The value of ![]() was first measured by Henry Cavendish in 1798 using a torsion balance experiment.
was first measured by Henry Cavendish in 1798 using a torsion balance experiment.
Gravitational Force and Field of Attraction
A gravitational field is a region around a mass where its gravitational influence can be felt. That is, the gravitational field strength at a point in space is defined as the force per unit mass at that point and is given by:
![]()
where:
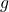 is the gravitational field strength,
is the gravitational field strength, is the mass of the object creating the field,
is the mass of the object creating the field, is the distance from the object’s center.
is the distance from the object’s center.
On Earth, the standard value of ![]() is approximately
is approximately ![]() , which causes objects to accelerate downward when dropped. Likewise, the gravitational field determines satellite motion and escape velocity.
, which causes objects to accelerate downward when dropped. Likewise, the gravitational field determines satellite motion and escape velocity.
Gravitational Field of a Hollow Spherical Shell in Space
A hollow spherical shell is a sphere with mass distributed uniformly on its surface but with an empty interior. Hence, to understand its gravitational field, we analyze two cases:
- Outside the Shell (
 )
) - Inside the Shell (
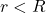 )
)
where:
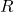 is the radius of the spherical shell.
is the radius of the spherical shell. is the distance from the center of the shell to the point where the field is being measured.
is the distance from the center of the shell to the point where the field is being measured.
Case 1: Gravitational Field Outside the Shell ( )
)
According to Newton’s Shell Theorem, a uniform spherical shell behaves like a point mass when observed from outside. That is, for a test mass ![]() located at a distance
located at a distance ![]() from the center, the gravitational field is the same as if the entire mass
from the center, the gravitational field is the same as if the entire mass ![]() of the shell were concentrated at a single point at the center.
of the shell were concentrated at a single point at the center.
Derivation:
Firstly, from Newton’s Law of Universal Gravitation, the gravitational force on a test mass ![]() outside the shell is:
outside the shell is:
![]()
The gravitational field is defined as the force per unit mass:
![]()
This result is identical to the field due to a point mass ![]() , meaning that outside the shell, the shell behaves like a point mass located at its center.
, meaning that outside the shell, the shell behaves like a point mass located at its center.
Result:
![]()
- The field follows the inverse-square law.
- The field points radially toward the center of the shell.
Case 2: Gravitational Field Inside the Shell (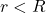 )
)
In short, a remarkable result of the Shell Theorem is that the gravitational field inside a uniform hollow shell is exactly zero everywhere.
Proof Using Symmetry and Gauss’s Law:
- Firstly, consider a test mass
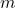 placed inside the shell at some point.
placed inside the shell at some point. - Then, the mass elements of the shell exert gravitational forces on the test mass.
- Due to symmetry, every mass element on one side of the test mass has a corresponding mass element on the opposite side exerting an equal and opposite force.
- Finally, the net effect of all these forces cancels out, leading to zero gravitational field at every point inside.
Mathematically, using Gauss’s Law for Gravity, the flux of gravitational field through a Gaussian surface inside the shell is zero because there is no enclosed mass. Since flux is proportional to gravitational field strength, we conclude that:
![]()
Result:
- Hence, a test mass inside the hollow shell experiences no gravitational force.
- Therefore, an object placed inside the shell will remain at rest or move with constant velocity (inertia).
This result has profound implications in astrophysics, as large spherical shells of mass (such as spherical galaxies) exert no force on objects inside them, which affects the motion of stars and cosmic structures.
Newton’s Law of Gravitation: Acceleration Due to Gravity
Acceleration due to gravity ![]() on the surface of a planet depends on its mass and radius and is given by:
on the surface of a planet depends on its mass and radius and is given by:
![]()
where ![]() is the planet’s mass and
is the planet’s mass and ![]() is its radius. To clarify, this equation shows that gravity varies across different planets and celestial bodies.
is its radius. To clarify, this equation shows that gravity varies across different planets and celestial bodies.

Relationship Between Acceleration Due to Gravity and Gravitational Field
The concepts of acceleration due to gravity and gravitational field are closely related and, in fact, represent the same physical quantity but in different contexts.
1. Definition of Gravitational Field
Since we know, the gravitational field at a point in space is the force per unit mass experienced by a small test mass placed at that point. Mathematically, it is defined as:
![]()
where:
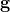 is the gravitational field (vector quantity).
is the gravitational field (vector quantity).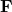 is the gravitational force experienced by a test mass
is the gravitational force experienced by a test mass 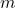 .
.- The unit of
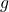 is N/kg (Newton per kilogram).
is N/kg (Newton per kilogram).
From Newton’s Law of Universal Gravitation, the force on a test mass ![]() due to a larger mass
due to a larger mass ![]() at a distance
at a distance ![]() is:
is:
![]()
Then, dividing by ![]() , we obtain the gravitational field:
, we obtain the gravitational field:
![]()
Thus, the gravitational field due to a mass ![]() is the acceleration that any object would experience due to the gravitational attraction of
is the acceleration that any object would experience due to the gravitational attraction of ![]() .
.
2. Acceleration Due to Gravity
The acceleration due to gravity ![]() at a point is the acceleration experienced by an object in free fall under the influence of gravity alone.
at a point is the acceleration experienced by an object in free fall under the influence of gravity alone.
Since force causes acceleration (Newton’s Second Law: ![]() ), we can express the acceleration due to gravity as:
), we can express the acceleration due to gravity as:
![]()
Since the gravitational force is:
![]()
Dividing by ![]() :
:
![]()
Thus, we see that:
![]()
This means that the gravitational field strength and the acceleration due to gravity are numerically identical but conceptually different.
The only two things you can truly depend upon are gravity and greed.
– Jack Palance
Acceleration Due to Gravity Above and Below Earth’s Surface
The acceleration due to gravity, ![]() , varies with altitude (
, varies with altitude (![]() ) and depth (
) and depth (![]() ).
).
1. At Earth’s Surface
![]()
where:
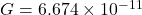
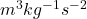 (gravitational constant)
(gravitational constant)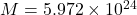
 (mass of Earth)
(mass of Earth)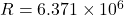
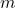 (radius of Earth)
(radius of Earth)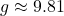

2. Above Earth’s Surface (h>0h > 0)
![]()
Additionally, for small heights (![]() ), an approximation:
), an approximation:
![]()
3. Below Earth’s Surface (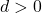 )
)
Since the field inside a spherical shell is zero, only the enclosed mass at radius ![]() contributes to gravity:
contributes to gravity:
![]()
or,
![]()
At Earth’s center (![]() ),
), ![]() .
.
You can’t blame gravity for falling in love.
– Albert Einstein
Example Numerical Problems on Newton’s Law of Gravitation with Solutions
Problem 1: Calculating the Gravitational Force
Question:
If two objects of masses 5 kg and 10 kg are placed 2 m apart, then, find the gravitational force between them.
Solution:
![]()
![]()
![]()
Problem 2: Acceleration Due to Gravity at a Height
Question:
Find the acceleration due to gravity at a height of 500 km above Earth’s surface. Take Earth’s radius as 6371 km and ![]() .
.
Solution:
![]()
![]()
Problem 3: Gravitational Field Inside a Hollow Sphere
Question:
What is the gravitational field inside a hollow sphere of mass 1000 kg and radius 10 m?
Solution:
Since, inside a hollow sphere, the net gravitational force is zero, the gravitational field is also zero.
Problem 4: Gravity Below Earth’s Surface
Question:
Find the acceleration due to gravity at a depth of 1000 km below the Earth’s surface.
Solution:
![]()
![]()
Problem 5: Mass of Earth from Gravity
Question:
If ![]() and
and ![]() , find the mass of Earth.
, find the mass of Earth.
Solution:
![]()
![]()
FAQs
1. Does gravity act in space?
Yes, gravity exists everywhere in space, but its strength decreases with distance.
2. Why don’t we feel gravitational attraction between small objects?
Since ![]() is very small, the gravitational force between small objects is negligible.
is very small, the gravitational force between small objects is negligible.
3. How does gravity affect time?
Newton’s law of gravity does not predict any variance in time. However, gravity affects time by slowing it down, an effect known as gravitational time dilation, predicted by Einstein’s General Theory of Relativity.
4. Can gravity be shielded?
Unlike electromagnetic forces, gravity cannot be shielded or blocked.
5. Why is newton’s law of gravitation important?
Because gravity holds planets in orbit, enables life on Earth, it plays a crucial role in the structure of the universe.
Conclusion
Newton’s Law of Gravity explains how masses interact across vast distances and governs planetary motion, satellite dynamics, and astrophysics. Hence, understanding gravity allows us to explore and appreciate the universe.
References
- Gron, Ø. (2009). Newton’s Law of Universal Gravitation. Lecture Notes in Physics. https://doi.org/10.1007/978-0-387-88134-8_1
- Borghi, R. (2014). On Newton’s Shell Theorem. European Journal of Physics, 35(2). https://doi.org/10.1088/0143-0807/35/2/028003
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W. H. Freeman and Company. ISBN: 978-0-7167-0344-0.
- Symon, K. R. (1971). Mechanics (3rd ed.). Addison-Wesley. ISBN: 978-0-201-07392-8.
Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.
