Collisions in Two Dimensions: The Physics behind Elastic and Inelastic Collisions
Estimated reading time: 12 minutes
Collisions are fundamental interactions in physics, occurring when two or more bodies exert forces on each other in a short period. From billiard balls striking one another to car crashes and subatomic particle interactions, collisions are ubiquitous in nature and engineering. Understanding collisions requires a grasp of conservation laws, vectors, and energy principles. This article delves into the mechanics of two-dimensional collisions in physics, exploring their types, governing laws, and mathematical formulation.
What are Collisions in Physics?
Collisions in physics refer to interactions where two or more objects exert forces on each other for a short duration, leading to changes in their motion. Hence, these interactions play a crucial role in various physical phenomena, from everyday occurrences like car crashes and sports impacts to atomic and celestial collisions.
Types of Collisions
In Physics, since collisions are classified based on how they conserve kinetic energy:
Elastic Collisions:
- Both linear momentum and kinetic energy are conserved.
- Hence, no energy is lost as heat or deformation.
Inelastic Collisions:
- Linear Momentum is conserved, but kinetic energy is not.
- Hence, some energy is converted into heat, sound, or deformation.
Perfectly Inelastic Collisions:
- A special case where objects stick together after impact.
- Maximum kinetic energy loss while conserving linear momentum.
One-Dimensional vs. Two-Dimensional Collisions
- One-Dimensional Collisions: Motion is along a single axis (e.g., a head-on collision between two balls).
- Two-Dimensional Collisions: Motion occurs in both x and y directions, requiring vector analysis to resolve velocity components.
Applications of Collision Physics
- Automobile Safety: Crumple zones absorb energy in inelastic collisions to reduce impact forces.
- Sports Physics: Elastic collisions determine ball rebounds in billiards and table tennis.
- Astrophysics: Planetary formation and asteroid impacts involve high-energy collisions.
Life is a series of collisions with the future; it is not the sum of what we have been, but what we yearn to be.
– Jose Ortega y Gasset
Also Read: Introduction to Particle Physics for High-School Students
3. Conservation Laws
Momentum Conservation During Collisions
Momentum is a fundamental quantity in physics that remains conserved in all types of collisions, provided there is no external force acting on the system. The principle of conservation of momentum states:
![]()
Mathematically, for a system of two colliding objects:
![]()
where:
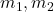 are the masses of the objects,
are the masses of the objects,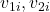 are the initial velocities,
are the initial velocities,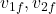 are the final velocities after the collision.
are the final velocities after the collision.
This principle holds true for both elastic and inelastic collisions.
Momentum Conservation in Different Types of Collisions
1. Elastic Collisions
- Both momentum and kinetic energy are conserved.
- Example: Two billiard balls colliding.
For a 1D elastic collision, the system of equations is:
![]()
![]()
These two equations help solve for the final velocities.
2. Inelastic Collisions
- Momentum is conserved, but kinetic energy is not.
- Example: A car crash where the cars crumple upon impact.
Momentum conservation equation:
![]()
However, kinetic energy before and after the collision differs because some energy is converted into heat, sound, or deformation.
3. Perfectly Inelastic Collisions
- Momentum is conserved, but kinetic energy loss is maximum.
- The objects stick together after collision and move as a single mass.
Momentum conservation equation:
![]()
where ![]() is the final velocity of the combined mass.
is the final velocity of the combined mass.
Momentum Conservation in Two-Dimensional Collisions
For collisions in two dimensions, momentum is conserved separately in the x and y directions:
![]()
![]()
To find the final velocities, we use vector addition:
![]()
Example Problem: Momentum Conservation in an Elastic Collision
A 2 kg ball moving at 3 m/s collides elastically with a 4 kg ball at rest. Find their velocities after collision.
Using the momentum and energy conservation equations, we can solve for ![]() and
and ![]() .
.
Answer:
Firstly, apply Momentum Conservation
The total momentum before and after the collision must be equal:
![]()
Substituting values:
![]()
![]()
![]()
Secondly, apply Kinetic Energy Conservation
Since the collision is elastic, kinetic energy is also conserved:
![]()
Cancel out ![]() from all terms:
from all terms:
![]()
Substituting values:
![]()
![]()
![]()
Finally, solve for 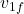 and
and 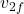
From Equation (1):
![]()
Substituting into Equation (2):
![]()
Expanding:
![]()
![]()
Factor:
![]()
So,
![]()
If ![]() , then from Equation (1),
, then from Equation (1), ![]() , which contradicts our assumption of interaction.
, which contradicts our assumption of interaction.
So, we take ![]() , and plug it into Equation (1):
, and plug it into Equation (1):
![]()
Therefore, Final Answer:
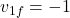 m/s (ball 1 moves in the opposite direction)
m/s (ball 1 moves in the opposite direction)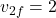 m/s (ball 2 moves forward)
m/s (ball 2 moves forward)
This means after the collision, the first ball rebounds in the opposite direction at 1 m/s, and the second ball moves forward at 2 m/s.
Energy Conservation During Collisions
In physics, during any collision, energy is always conserved, but the way kinetic energy behaves depends on the type of collision.
The total energy of a system before and after a collision remains constant. This includes:
- Kinetic Energy (KE): Energy due to motion
- Potential Energy (PE): Energy due to position
- Heat, Sound, and Deformation Energy (in inelastic collisions)
However, whether kinetic energy is conserved or not depends on the type of collision.
Kinetic Energy in Different Types of Collisions
(A) Elastic Collisions
- Both momentum and kinetic energy are conserved.
- No energy is lost to heat, sound, or deformation.
- Example: Billiard ball collisions, gas molecules in an ideal gas.
Mathematically:
![]()
Hence, this equation, along with momentum conservation, helps find post-collision velocities.
(B) Inelastic Collisions
- Momentum is conserved, but kinetic energy is not.
- Consequently, some kinetic energy is converted into heat, sound, or deformation.
- Example: A clay ball hitting the ground and sticking.
![]()
Only momentum conservation applies:
![]()
(C) Perfectly Inelastic Collisions
- Momentum is conserved, but kinetic energy loss is maximum.
- The two objects stick together and move as one mass.
- Example: A car crash where cars lock together.
Momentum conservation:
![]()
Kinetic energy is always lost:
![]()
![]()
The lost energy is transformed whether into heat, sound, or internal deformation.
Example Problem: Energy in a Perfectly Inelastic Collision
A 5 kg object moving at 6 m/s collides with a 3 kg object at rest. If they stick together find the final velocity and energy lost.
Firstly, Apply Momentum Conservation
![]()
![]()
Secondly, calculate Initial and Final KE
![]()
![]()
Hence, final KE:
![]()
![]()
Finally, find Energy Lost
![]()
So, 33.75 J of energy was lost, transformed into heat, sound, and deformation.
Key Takeaways
- Elastic Collisions: Both kinetic energy and momentum conserved.
- Inelastic Collisions: Only momentum conserved, kinetic energy partially lost.
- Perfectly Inelastic Collisions: Maximum kinetic energy lost. The objects stick together.
8. Example Problems
8.1 Elastic Collisions
Problem 1
Two balls, mass 2 kg and 3 kg, collide elastically. If the first moves at 4 m/s along x-axis, the second at 2 m/s along y-axis, then find final velocities.
Solution
Since:
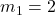 kg,
kg, 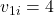 m/s along x-axis
m/s along x-axis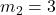 kg,
kg, 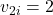 m/s along y-axis
m/s along y-axis
Momentum is conserved in both x and y directions:
![]()
![]()
Since ![]() and
and ![]() , we solve separately:
, we solve separately:
![]()
![]()
Then, using kinetic energy conservation:
![]()
Finally,
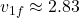 m/s
m/s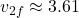 m/s
m/s
at angles based on conservation laws.
Problem 2
A ball of 0.5 kg moving at 3 m/s strikes another stationary identical ball. Then, find their velocities post-collision.
Solution
Since:
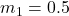 kg,
kg, 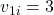 m/s
m/s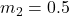 kg,
kg, 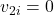
Hence, final velocities (elastic collision formula for identical masses):
![]()
![]()
So, the first ball stops, and the second moves at 3 m/s.
Problem 3
If, two identical ice pucks collide at 45-degree angles with initial speeds of 2 m/s, then find their final speeds.
Solution
Since:
- Identical pucks,
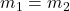 ,
, 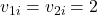 m/s
m/s - Collision at 45° angles
Using conservation of momentum in both axes and symmetry,
![]()
Hence, they move at right angles to their original paths.
8.2 Inelastic Collisions
Problem 4
A 3 kg ball moving at 5 m/s hits a 4 kg ball at rest. If they stick together, find their final velocity.
Solution
Since:
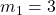 kg,
kg, 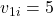 m/s
m/s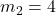 kg,
kg, 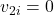 m/s
m/s
Then using momentum conservation:
![]()
![]()
![]()
![]()
Therefore, Final velocity = ![]() m/s (both move together).
m/s (both move together).
Problem 5
Two ice skaters collide and move together. If one has a velocity of 3 m/s, the other is stationary find their velocity post-collision.
Solution
Since:
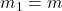 ,
, 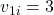 m/s
m/s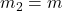 ,
, 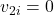
Since they stick together:
![]()
![]()
![]()
Therefore, Final velocity = ![]() m/s (both move together).
m/s (both move together).
Problem 6
If a bullet of mass 0.1 kg moving at 500 m/s embeds itself in a wooden block of mass 1 kg, find their velocity after collision.
Solution
Since:
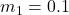 kg,
kg, 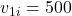 m/s
m/s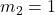 kg,
kg, 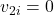
Firstly, using momentum conservation:
![]()
![]()
![]()
![]()
Hence, Final velocity = ![]() m/s (both move together).
m/s (both move together).
FAQs
1. What is the main difference between elastic and inelastic collisions in physics?
Ans: In elastic collisions, both momentum and kinetic energy are conserved, whereas in inelastic collisions, only momentum is conserved, and kinetic energy is partially lost.
2. How do we analyze a collision in two dimensions?
Ans: Firstly, we break the motion into x- and y-components and then apply the conservation of momentum separately in each direction.
3. Why is kinetic energy not always conserved in a collision?
Ans: Some of the kinetic energy is converted into heat, sound, or deformation of objects, especially in inelastic collisions.
4. What role do vectors play in two-dimensional collisions?
Ans: Since motion occurs in multiple directions, momentum is treated as a vector quantity, requiring vector addition and decomposition.
5. Can a completely inelastic collision still conserve total energy?
Ans: Yes, while kinetic energy is lost, total mechanical energy (including other forms like heat or deformation) remains conserved.
6. What is an example of an elastic collision in real life?
Ans: A collision between billiard balls is nearly elastic since they retain most of their kinetic energy.
7. How does mass affect the outcome of a two-dimensional collision?
Ans: Heavier objects tend to change velocity less upon impact, while lighter ones experience more noticeable deflections.
8. How does the angle of impact influence the final motion of colliding objects?
Ans: The angle determines how momentum is distributed between x- and y-components, and consequently affects the direction and speed after collision.
9. What happens when two objects of equal mass collide elastically at an angle?
Ans: If one object was initially at rest, they typically move at 90° angles after collision, following the momentum conservation laws.
10. Why do we use the center of mass frame in collision analysis?
Ans: It simplifies calculations because it allows us to analyze motion relative to the system’s moving center of mass, making conservation laws easier to apply.
Conclusion
Collisions in two dimensions are essential in physics, governing interactions from microscopic particles to large-scale astrophysical events. Understanding momentum and energy conservation allows us to predict post-collision motion in both elastic and inelastic cases. Unlike one-dimensional collisions, two-dimensional cases require vector analysis, making problem-solving more complex but also more applicable to real-world scenarios like car crashes, sports dynamics, and space object interactions. Hence, by applying conservation laws, we can analyze and solve practical collision problems in physics, reinforcing their significance in physics and engineering.
References
- Burko, L. M. (2019). Two-Dimensional Collisions and Conservation of Momentum. The Physics Teacher, 57(7), 487-489. https://doi.org/10.1119/1.5126832
- Ogura, A. (2018). Diagrammatic Approach for Investigating Two Dimensional Elastic Collisions in Momentum Space I: Newtonian Mechanics. World Journal of Mechanics, 8(9), 343-352. https://doi.org/10.4236/wjm.2018.89025
- Burton, J. C., Lu, P. Y., & Nagel, S. R. (2013). Collision Dynamics of Particle Clusters in a Two-Dimensional Granular Gas. Physical Review E, 88(6), 062204. https://doi.org/10.1103/PhysRevE.88.062204
Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.
