Exploring Einstein’s Special Theory of Relativity: A Brief Overview
Einstein’s theory of Special Relativity, published in 1905, revolutionized our understanding of space and time. It emerged from the need to reconcile the laws of electromagnetism with the principles of classical mechanics. This theory introduced profound changes to the concepts of space and time, leading to phenomena such as time dilation, length contraction, and the equivalence of mass and energy.
Disagreement Between Classical Mechanics and Electromagnetism
Classical mechanics, based on Newton’s laws, assumes that time and space are absolute. However, Maxwell’s equations of electromagnetism suggested that the speed of light is constant in all inertial frames. Thus, this discrepancy led Einstein to propose that the laws of physics are the same in all inertial frames and that the speed of light is invariant, regardless of the observer’s motion.
When you are courting a nice girl an hour seems like a second. When you sit on a red-hot cinder a second seems like an hour. That’s relativity.
– Albert Einstein
Lorentz Transformation in Einstein’s theory of Special Relativity
The Lorentz transformation is the cornerstone of Einstein’s Special Relativity. In short, it describes how measurements of space and time by two observers moving at a constant velocity relative to each other are related. Unlike the Galilean transformation of classical mechanics, the Lorentz transformation preserves the speed of light as a constant in all inertial frames. This section will delve into the mathematical formulation of the Lorentz transformation and its physical implications, including time dilation, length contraction, and proper time.
Time Dilation in Einstein’s theory of Special Relativity
Einstein’s theory of Special Relativity has one of the most noticeable effects of the Lorentz transformation is that time slows down. It says that a clock that is moving in relation to a person will look like it ticks more slowly than a clock that is still in that person’s frame. This happens because time intervals are not fixed and rely on how fast or slow the observer and the clock are moving.
Mathematical Derivation
If you were to consider two inertial frames ![]() and
and ![]() , where
, where ![]() is moving with a constant velocity
is moving with a constant velocity ![]() along the
along the ![]() -axis relative to
-axis relative to ![]() . Then, the Lorentz transformation for time is given by:
. Then, the Lorentz transformation for time is given by:
![]()
where ![]() is the Lorentz factor.
is the Lorentz factor.
Suppose a clock is at rest in frame ![]() (i.e.,
(i.e., ![]() ). Then, the time interval
). Then, the time interval ![]() measured in
measured in ![]() is related to the time interval
is related to the time interval ![]() measured in
measured in ![]() by:
by:
![]()
Thus, this shows that ![]() , meaning time appears to run slower in the moving frame.
, meaning time appears to run slower in the moving frame.
Example
If a spaceship travels at ![]() , and 1 year passes on the spaceship (
, and 1 year passes on the spaceship (![]() ), the time elapsed on Earth (
), the time elapsed on Earth (![]() ) is:
) is:
![]()
Length Contraction in Einstein’s theory of Special Relativity
Einstein’s theory of Special Relativity has one more effect of the Lorentz change is that length gets shorter. There is a rule that says an item that is moving will look shorter along the direction of motion than it was in its rest frame.
Mathematical Derivation
Consider a rod of proper length ![]() (length in its rest frame
(length in its rest frame ![]() ). Then in frame
). Then in frame ![]() , where the rod is moving with velocity
, where the rod is moving with velocity ![]() , the length
, the length ![]() is given by:
is given by:
![]()
This arises because the positions of the ends of the rod must be measured simultaneously in frame ![]() , and the Lorentz transformation affects these measurements.
, and the Lorentz transformation affects these measurements.
Example
If a rod has a proper length of ![]() and moves at
and moves at ![]() , its length in the lab frame is:
, its length in the lab frame is:
![]()
Proper Time in Einstein’s theory of Special Relativity
Proper time in Einstein’s theory of Special Relativity is the time interval measured by a clock in its own rest frame. It is an invariant quantity, meaning all observers will agree on its value, regardless of their relative motion.
Mathematical Derivation
If you consider a clock moving with velocity ![]() in frame
in frame ![]() . Then the proper time interval
. Then the proper time interval ![]() is related to the coordinate time interval
is related to the coordinate time interval ![]() in frame
in frame ![]() by:
by:
![]()
This relationship arises because the clock’s time is “dilated” in the moving frame.
Example
A muon travels ![]() in the lab frame at
in the lab frame at ![]() . The time elapsed in the lab frame is:
. The time elapsed in the lab frame is:
![]()
The proper time experienced by the muon is:
![]()
Lorentz Transformation Equations
The full set of Lorentz transformation equations relates the coordinates ![]() in frame
in frame ![]() to the coordinates
to the coordinates ![]() in frame
in frame ![]() :
:
![]()
![]()
![]()
![]()
Thus, these equations ensure that the speed of light ![]() is the same in all inertial frames.
is the same in all inertial frames.
Invariance of the Spacetime Interval
The spacetime interval ![]() is an invariant quantity under Lorentz transformations. Hence, it is defined as:
is an invariant quantity under Lorentz transformations. Hence, it is defined as:
![]()
In another inertial frame ![]() , the interval is:
, the interval is:
![]()
In short, the invariance of ![]() means that
means that ![]() , which is a fundamental property of spacetime in Special Relativity.
, which is a fundamental property of spacetime in Special Relativity.
Relativistic Velocity Addition
The Lorentz transformation also affects how velocities add. If an object has velocity ![]() in frame
in frame ![]() , its velocity
, its velocity ![]() in frame
in frame ![]() is given by:
is given by:
![]()
Thus, this formula ensures that the speed of light is not exceeded.
Example
If a spaceship moves at ![]() relative to Earth and emits a particle at
relative to Earth and emits a particle at ![]() in its own frame, the particle’s velocity in Earth’s frame is:
in its own frame, the particle’s velocity in Earth’s frame is:
![]()
Physical Interpretation
In Einstein’s theory of Special Relativity, the Lorentz transformation reveals that space and time are intertwined into a single entity called spacetime. Measurements of time intervals and lengths depend on the observer’s motion, but the spacetime interval remains invariant. Therefore, this unification of space and time is a central theme in Special Relativity.
Lagrangian Mechanics in Einstein’s theory of Special Relativity
Lagrangian mechanics provides a powerful and elegant framework for analyzing physical systems, particularly in the context of Special Relativity. It is based on the principle of least action, which states that the path taken by a system between two points in spacetime is the one that minimizes the action. In this section, we will explore the role of Lagrangian mechanics in Special Relativity, including the derivation of the relativistic Lagrangian, the Euler-Lagrange equation, and the connection to momentum and energy.
Variation in Action
The action ![]() is a fundamental quantity in Lagrangian mechanics. Consequently, defined as the integral of the Lagrangian
is a fundamental quantity in Lagrangian mechanics. Consequently, defined as the integral of the Lagrangian ![]() over time:
over time:
![]()
The principle of least action states that the actual path taken by a system between two points in spacetime is the one that minimizes (or extremizes) the action. Hence, mathematically expressed as:
![]()
where ![]() represents the variation in the action.
represents the variation in the action.
Lagrangian Theory
In classical mechanics, the Lagrangian ![]() is typically defined as the difference between the kinetic energy
is typically defined as the difference between the kinetic energy ![]() and the potential energy
and the potential energy ![]() :
:
![]()
However, in Special Relativity, the Lagrangian must be modified to account for relativistic effects. Hence, for a free particle (no potential energy), the relativistic Lagrangian is:
![]()
where ![]() is the rest mass of the particle,
is the rest mass of the particle, ![]() is its velocity, and
is its velocity, and ![]() is the speed of light.
is the speed of light.
Fun Fact: The famous equation (
) means a single gram of mass could power 21,000 tons of TNT! 💥🔬
Derivation of the Relativistic Lagrangian
The relativistic Lagrangian can be derived by requiring that the action ![]() be Lorentz invariant. If a free particle moves in spacetime, the action must depend only on the spacetime interval
be Lorentz invariant. If a free particle moves in spacetime, the action must depend only on the spacetime interval ![]() , which is invariant under Lorentz transformations. Then the action defined as:
, which is invariant under Lorentz transformations. Then the action defined as:
![]()
where ![]() is the infinitesimal spacetime interval:
is the infinitesimal spacetime interval:
![]()
Expressing ![]() in terms of the particle’s velocity
in terms of the particle’s velocity ![]() , we get:
, we get:
![]()
Thus, the action becomes:
![]()
Hence, comparing this with the definition of the action ![]() , we identify the relativistic Lagrangian as:
, we identify the relativistic Lagrangian as:
![]()
Euler-Lagrange Equation
The Euler-Lagrange equation is the fundamental equation of motion in Lagrangian mechanics. Consequently, for a system with generalised coordinates ![]() , the Euler-Lagrange equation is:
, the Euler-Lagrange equation is:
![]()
For a free particle in Special Relativity, the Lagrangian depends only on the velocity ![]() , so the Euler-Lagrange equation simplifies to:
, so the Euler-Lagrange equation simplifies to:
![]()
Hence, this implies that the generalized momentum ![]() is conserved.
is conserved.
Hamiltonian in Einstein’s theory of Special Relativity
The Hamiltonian ![]() represents the total energy of a system. Hence, it is related to the Lagrangian by the Legendre transformation:
represents the total energy of a system. Hence, it is related to the Lagrangian by the Legendre transformation:
![]()
where ![]() is the generalized momentum.
is the generalized momentum.
Therefore, for a free relativistic particle, the Hamiltonian is:
![]()
where ![]() . This represents the total energy of the particle, including its rest energy
. This represents the total energy of the particle, including its rest energy ![]() and kinetic energy.
and kinetic energy.
In Einstein’s general relativity the structure of space can change but not its topology. Topology is the property of something that doesn’t change when you bend it or stretch it as long as you don’t break anything.
– Edward Witten
Energy and Momentum in Special Relativity
Einstein’s theory of special relativity has a huge impact on how we think about energy and motion, which are two very important ideas in physics. We will also look at how energy and momentum are defined in relativity, the famous mass-energy equation ![]() , and talk about a photon’s momentum. In the setting of Special Relativity, we will also look at how energy, momentum, and mass are related.
, and talk about a photon’s momentum. In the setting of Special Relativity, we will also look at how energy, momentum, and mass are related.
Derivation of Relativistic Momentum
In classical mechanics, momentum is defined as ![]() , where
, where ![]() is the mass and
is the mass and ![]() is the velocity. However, in Einstein’s theory of Special Relativity, momentum must be redefined to account for the effects of high velocities.
is the velocity. However, in Einstein’s theory of Special Relativity, momentum must be redefined to account for the effects of high velocities.
Relativistic Momentum
The relativistic momentum ![]() of a particle given by:
of a particle given by:
![]()
where ![]() is the Lorentz factor,
is the Lorentz factor, ![]() is the rest mass, and
is the rest mass, and ![]() is the velocity. This definition ensures that momentum increases without bound as the velocity approaches the speed of light.
is the velocity. This definition ensures that momentum increases without bound as the velocity approaches the speed of light.
Derivation
The relativistic momentum can be derived from the relativistic Lagrangian ![]() . The generalized momentum is:
. The generalized momentum is:
![]()
This shows that the momentum depends on the velocity in a nonlinear way, reflecting the effects of Special Relativity.
Mass-Energy Equivalence 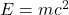
One of the most famous results of Einstein’s theory of Special Relativity is the mass-energy equivalence equation ![]() . This equation states that energy and mass are interchangeable.
. This equation states that energy and mass are interchangeable.
Total Energy of a Particle
The total energy ![]() of a particle given by:
of a particle given by:
![]()
where ![]() is the Lorentz factor. Hence, for a particle at rest (
is the Lorentz factor. Hence, for a particle at rest (![]() ), this reduces to:
), this reduces to:
![]()
Hence, this is the rest energy of the particle, i.e. the energy equivalent of its mass.
Derivation
The total energy can be derived from the relativistic Hamiltonian ![]() , which represents the total energy of the system. Hence, for a free particle, the Hamiltonian is:
, which represents the total energy of the system. Hence, for a free particle, the Hamiltonian is:
![]()
This includes both the rest energy ![]() and the kinetic energy
and the kinetic energy ![]() .
.
Energy-Momentum Relation in Special Relativity
The total energy ![]() and momentum
and momentum ![]() of a particle are related by the energy-momentum relation:
of a particle are related by the energy-momentum relation:
![]()
In short, this equation is a cornerstone of Special Relativity and connects the concepts of energy, momentum, and mass.
Derivation
Firstly, from the definitions of relativistic energy and momentum:
![]()
we can eliminate ![]() to obtain the energy-momentum relation. Squaring both equations and subtracting, we get:
to obtain the energy-momentum relation. Squaring both equations and subtracting, we get:
![]()
Thus:
![]()
Momentum of a Photon
A photon is a massless particle that always travels at the speed of light ![]() . Despite having no rest mass, a photon carries momentum.
. Despite having no rest mass, a photon carries momentum.
Relativistic Momentum of a Photon
The momentum ![]() of a photon is related to its energy
of a photon is related to its energy ![]() by:
by:
![]()
This relationship arises because the energy-momentum relation for a massless particle (![]() ):
):
![]()
Example
Thus, for a photon with energy ![]() , the momentum is:
, the momentum is:
![]()
Kinetic Energy in Special Relativity
The kinetic energy ![]() of a relativistic particle is the total energy minus the rest energy:
of a relativistic particle is the total energy minus the rest energy:
![]()
For small velocities (![]() ), this reduces to the classical expression:
), this reduces to the classical expression:
![]()
Conclusion
In conclusion, Einstein’s Special Relativity has profoundly transformed our understanding of space, time, and energy. Consequently, by reconciling electromagnetism with mechanics, it introduced concepts like time dilation, length contraction, and mass energy equivalence. Hence, the Special Theory’s mathematical elegance and experimental validation continue to inspire advancements in physics.
Therefore, by exploring the relativistic definitions of energy and momentum, we gain a deeper appreciation for the profound changes that Special Relativity brings to our understanding of the physical world. These concepts are not only significant on paper but also have practical applications in fields ranging from particle physics to astrophysics.
FAQ’s
1. What is time dilation in Special Relativity, and how does it work?
Answer:
Time dilation is a phenomenon where time moves slower for an object in motion compared to a stationary observer.
✔ Key Formula:
![Rendered by QuickLaTeX.com \[\Delta t = \gamma \Delta t' \quad \text{where} \quad \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]](https://entechonline.com/wp-content/ql-cache/quicklatex.com-67d4bd3d327a779608101842154203d9_l3.png)
- (
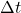 ): Time measured by a stationary observer
): Time measured by a stationary observer - (
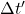 ): Time measured by a moving observer
): Time measured by a moving observer - (v): Relative velocity
- (c): Speed of light
Example:
If a spaceship travels at 80% the speed of light ![]() :
:
- 1 year on the ship
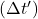 = 1.67 years on Earth
= 1.67 years on Earth  .
.
Real-World Proof: GPS satellites adjust for time dilation to maintain accuracy!
2. Why can’t anything travel faster than light?
Answer:
Special Relativity imposes this limit because:
- Mass-Energy Equivalence (
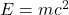 ): As an object approaches (c), its relativistic mass increases, requiring infinite energy to accelerate further.
): As an object approaches (c), its relativistic mass increases, requiring infinite energy to accelerate further. - Causality Violation: Faster-than-light travel could reverse cause-and-effect (e.g., an effect occurring before its cause).
Mathematical Insight:
The Lorentz factor (![]() ) becomes imaginary for (v > c), breaking physical laws.
) becomes imaginary for (v > c), breaking physical laws.
Did You Know? Particles like photons travel at (![]() ) precisely because they’re massless!
) precisely because they’re massless!
References
- Shan, X., Hu, B., Chen, X. et al. An interference-based method for the detection of strongly lensed gravitational waves. Nat Astron (2025). https://doi.org/10.1038/s41550-025-02519-5
- Maceda, M.D., Sabín, C. Digital quantum simulation of cosmological particle creation with IBM quantum computers. Sci Rep 15, 3476 (2025). https://doi.org/10.1038/s41598-025-87015-6
- Calzà, M., Gianesello, F., Rinaldi, M. et al. Implications of cosmologically coupled black holes for pulsar timing arrays. Sci Rep 14, 31296 (2024). https://doi.org/10.1038/s41598-024-82661-8
- Dreissen, L.S., Yeh, CH., Fürst, H.A. et al. Improved bounds on Lorentz violation from composite pulse Ramsey spectroscopy in a trapped ion. Nat Commun 13, 7314 (2022). https://doi.org/10.1038/s41467-022-34818-0
Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. Basically, this is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.

