Gravitational Potential Energy: Fields, Potential and Escape Velocity
Estimated reading time: 11 minutes
Gravity is one of the four fundamental forces of nature, governing the motion of celestial bodies and objects on Earth. Moreover, Newton’s Law of Universal Gravitation provides a mathematical framework for understanding gravitational interactions. In this article, we will explore Gravitational Potential Energy in depth, covering key concepts such as gravitational fields, escape velocity, and the energy of orbiting satellites.
Newton’s Law of Universal Gravitation
Newton’s Law of Universal Gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them:
![]()
where:
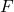 is the gravitational force,
is the gravitational force,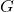 is the gravitational constant (
is the gravitational constant (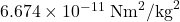 ),
),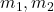 are the masses of the objects,
are the masses of the objects, is the distance between the centers of the masses.
is the distance between the centers of the masses.
Consequently, this law explains planetary motion, tides, and the motion of satellites around Earth.
What is a Gravitational Field?
A gravitational field is a region in space where a mass experiences a force due to gravity. Hence, it describes how the gravitational force is distributed around a massive object.
Definition of Gravitational Field
To clarify, the gravitational field strength at any point is defined as the force per unit mass experienced by a small test mass placed at that point. Hence, mathematically given by:
![]()
where:
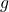 : the gravitational field strength (measured in N/kg\text{N/kg}N/kg or m/s2\text{m/s}^2m/s2),
: the gravitational field strength (measured in N/kg\text{N/kg}N/kg or m/s2\text{m/s}^2m/s2),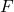 : the gravitational force,
: the gravitational force,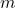 : the mass experiencing the force.
: the mass experiencing the force.
Gravitational Field Due to a Point Mass
Hence, for a mass ![]() , the gravitational field at a distance
, the gravitational field at a distance ![]() from its center is given by:
from its center is given by:
![]()
where:
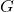 is the gravitational constant (
is the gravitational constant (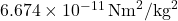 ),
), is the distance from the mass
is the distance from the mass  .
.
Therefore, this equation shows that the gravitational field decreases as the distance from the mass increases.
Gravitational Field Near Earth’s Surface
Near the Earth’s surface, the gravitational field strength is approximately:
![]()
Consequently, this means that any object in Earth’s gravitational field experiences an acceleration of 9.8 m/s² toward the Earth’s center.
Direction of the Gravitational Field
The gravitational field is always attractive, pointing toward the center of the mass creating the field.
Gravitational Potential Energy
Gravitational potential energy is the energy stored in an object due to its position in a gravitational field. That is, it represents the work done to bring an object from infinity to a given point against gravitational attraction.
Formula for Gravitational Potential Energy
For an object of mass ![]() at a distance
at a distance ![]() from a mass
from a mass ![]() , the gravitational potential energy is given by:
, the gravitational potential energy is given by:
![]()
where:
 = Gravitational potential energy (Joules,
= Gravitational potential energy (Joules, 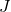 )
) = Gravitational constant (
= Gravitational constant (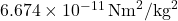 )
) = Mass of the larger body (kg)
= Mass of the larger body (kg)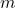 = Mass of the object (kg)
= Mass of the object (kg) = Distance from the center of the larger body (m)
= Distance from the center of the larger body (m)
Why is Gravitational Potential Energy Negative?
- Firstly, at infinity, gravitational potential energy
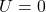
- As an object moves closer to the mass, energy is lost (i.e., energy is released).
- Since gravity is an attractive force, work must be done to move an object away from a mass, making GPE negative in bound systems.
Near-Earth Approximation
Near Earth’s surface, for small heights ![]() , we use the simpler formula:
, we use the simpler formula:
![]()
where:
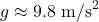 (acceleration due to gravity on Earth),
(acceleration due to gravity on Earth),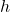 = height above the reference level.
= height above the reference level.
This approximation is valid when ![]() (Earth’s radius).
(Earth’s radius).
Difference Between Gravitational Potential and Gravitational Potential Energy
| Quantity | Gravitational Potential (V) | Gravitational Potential Energy (U) |
| Definition | Energy per unit mass | Energy stored in a mass due to gravity |
| Formula | V= -GM/r | U = -GMm/r |
| Units | Joules per kilogram (J/kg) | Joules (J) |
| Depends on | Mass creating the field | Mass of the object + mass of the field source |
Example Problem
Problem:
If the mass of a satellite orbiting Earth at an altitude of 500 km is 1000 kg, find the gravitational potential energy.
- Mass of Earth,
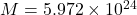 kg
kg - Radius of Earth,
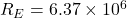 m
m - Distance from Earth’s center,
 m
m
Solution:
Since:
![]()
![]()
Hence, this means the satellite has a gravitational potential energy of ![]() J, indicating it is bound to Earth’s gravity.
J, indicating it is bound to Earth’s gravity.
Gravitational Potential Energy of a Sphere
When dealing with a solid sphere of mass ![]() and radius
and radius ![]() , its gravitational potential energy (
, its gravitational potential energy (![]() ) is calculated differently depending on whether we consider:
) is calculated differently depending on whether we consider:
- A point mass outside the sphere
- The self-gravitational potential energy of the sphere
1. Gravitational Potential Energy of a Mass Outside a Sphere
If a small mass ![]() is located at a distance
is located at a distance ![]() from the center of a uniform sphere of mass
from the center of a uniform sphere of mass ![]() , the gravitational potential energy is given by:
, the gravitational potential energy is given by:
![]()
First Case: Outside the Sphere ( )
)
- The sphere behaves as if all its mass is concentrated at a point at its center.
- The formula
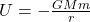 applies as if it were a point mass.
applies as if it were a point mass.
Second Case: On the Surface (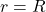 )
)
Third Case: Inside the Sphere (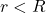 )
)
When inside a uniform sphere, only the mass enclosed within radius ![]() contributes to the gravitational force. Therefore, the effective gravitational potential energy at distance
contributes to the gravitational force. Therefore, the effective gravitational potential energy at distance ![]() inside the sphere is:
inside the sphere is:
![]()
2. Self-Gravitational Potential Energy of a Sphere
The self-gravitational potential energy is the energy required to assemble a sphere of mass ![]() and radius
and radius ![]() by bringing its mass together from infinity.
by bringing its mass together from infinity.
![]()
Consequently, this formula is derived by integrating the work required to bring infinitesimal mass shells together incrementally.
Key Takeaways:
- A hollow sphere has constant gravitational potential inside.
- A solid sphere exerts a gravitational pull inside it, and the potential energy follows a different equation as given above.
Example Calculation
Problem:
If mass ![]() kg and radius
kg and radius ![]() m, find the self-gravitational potential energy of Earth.
m, find the self-gravitational potential energy of Earth.
Solution:
![]()
Then, substituting values:
![]()
![]()
Hence, this means that assembling Earth from dispersed particles would require an energy input of ![]() Joules.
Joules.
Escape Velocity
Escape velocity is the minimum velocity an object must have to escape a celestial body’s gravitational field without any further propulsion. That is, at this velocity, the object’s kinetic energy is equal to the gravitational potential energy, allowing it to reach infinity with zero remaining energy.
Derivation of Escape Velocity
For an object of mass ![]() to escape from a planet of mass
to escape from a planet of mass ![]() and radius
and radius ![]() , the total energy at the surface should be zero at infinity.
, the total energy at the surface should be zero at infinity.
Total Energy at the Surface:
![]()
![]()
That is, for the object to escape, its total energy must be zero at infinity:
![]()
Then, canceling ![]() and solving for
and solving for ![]() :
:
![]()
where:
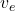 = Escape velocity (m/s)
= Escape velocity (m/s)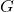 = Gravitational constant (
= Gravitational constant (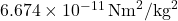 )
) = Mass of the celestial body (kg)
= Mass of the celestial body (kg)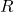 = Radius of the celestial body (m)
= Radius of the celestial body (m)
Escape Velocity of Earth
For Earth:
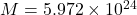 kg
kg m
m
![]()
![]()
Thus, an object must travel at 11.2 km/s (about 40,320 km/h) to escape Earth’s gravity.
Key Observations
- Escape velocity increases with mass (
 ) and decreases with radius (
) and decreases with radius (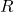 ).
). - A higher mass and smaller radius result in a higher escape velocity.
- The Moon has a low escape velocity (2.4 km/s), which is why it cannot retain an atmosphere like Earth.
- The Sun’s escape velocity is 617.5 km/s, meaning an object must move incredibly fast to leave the Sun’s gravity.
Relation to Orbital Velocity
Escape velocity is related to orbital velocity by:
![]()
where ![]() is the velocity required to stay in a circular orbit around the planet. Therefore, this means escape velocity is about 1.41 times the orbital velocity.
is the velocity required to stay in a circular orbit around the planet. Therefore, this means escape velocity is about 1.41 times the orbital velocity.
Example Problem
Problem:
Find the escape velocity for Mars.
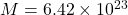 kg
kg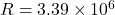 m
m
Solution:
![]()
![]()
So, the escape velocity for Mars is 5.0 km/s.
Interesting Facts
- Black holes have escape velocities greater than the speed of light (
 ). This is why not even light can escape them.
). This is why not even light can escape them. - Rockets do not need to reach escape velocity instantly. In short, they accelerate gradually using fuel over time.
- The Voyager 1 spacecraft is moving at ~17 km/s, which is much faster than Earth’s escape velocity, allowing it to leave the solar system. Consequently, this is known as the third cosmic velocity or interstellar speed.
Frequently Asked Questions
1. Why is gravitational potential always negative?
Gravitational potential is negative because work must be done against gravity to move a mass from a given point to infinity (where potential is defined as zero). Since gravity is always attractive, potential energy decreases as objects move closer, making it negative.
2. What is escape velocity, and why does it not depend on the escaping object’s mass?
Escape velocity is the minimum speed needed for an object to break free from a planet’s gravitational field without further propulsion. That is given by:
![]()
Since mass ![]() cancels out in the derivation, escape velocity depends only on the planet’s mass and radius, not on the mass of the escaping object.
cancels out in the derivation, escape velocity depends only on the planet’s mass and radius, not on the mass of the escaping object.
3. Can an object escape Earth’s gravity at a velocity lower than escape velocity?
Yes, but only with continuous propulsion (e.g., a rocket). Additionally, escape velocity applies to objects launched without excess thrust (like a projectile). Rockets gradually build up speed over time, rather than needing 11.2 km/s instantly.
4. Does escape velocity change with altitude?
Certainly, escape velocity is inversely proportional to the square root of distance from the center of the planet:
![]()
As altitude (![]() ) increases,
) increases,![]() also increases, so escape velocity decreases.
also increases, so escape velocity decreases.
5. How does gravitational potential energy change in a multi-body system (e.g., the Earth-Moon system)?
Gravitational potential energy is a pairwise additive quantity. That is, for multiple bodies, the total energy is the sum of individual interactions:
![]()
Hence, each term follows ![]() , accounting for the gravitational effect between each pair of bodies.
, accounting for the gravitational effect between each pair of bodies.
6. Why do astronauts in orbit feel weightless if gravity is still acting on them?
Astronauts feel weightless because they are in free fall around Earth. That is, the spaceship and astronauts accelerate toward Earth at the same rate, meaning there is no normal force acting on them, creating a sensation of weightlessness.
7. If a spacecraft reaches escape velocity, does it mean it will leave the solar system?
Not necessarily. Escape velocity is relative to a specific celestial body (e.g., Earth). Consequently, to leave the solar system, a spacecraft must achieve the Sun’s escape velocity at Earth’s distance, which is about 42.1 km/s (16.7 km/s counting speed of Earth’s revolution). This is much higher than Earth’s escape velocity (11.2 km/s).
Conclusion
In conclusion, understanding gravitational potential energy and its related concepts is essential for astrophysics, space exploration, and planetary science. Consequently, these principles help in predicting planetary motion, designing satellites, and understanding cosmic phenomena. Escape velocity is a crucial concept utilized in many practical situations such as the launching of satellites and rockets. Consequently, understanding the first, second and third cosmic velocities plays a crucial role in space exploration, now and in the future.
References
- Gron, Ø. (2009). Newton’s law of universal gravitation. In Lecture notes in physics. Springer. https://doi.org/10.1007/978-0-387-88134-8_1
- Borghi, R. (2014). On Newton’s shell theorem. European Journal of Physics, 35(2), 028003. https://doi.org/10.1088/0143-0807/35/2/028003
- Longuski, J., Hoots, F., & IV, G. (2021). The gravitational potential. In Introduction to orbital perturbations (pp. 143–171). Springer. https://doi.org/10.1007/978-3-030-89758-1_7
Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.
