Moment of Inertia: Formulae for Different Shapes

Published on: March 25, 2025in

It is a measure of an object's resistance to changes in its rotational motion.

Estimated reading time: 8 minutes

The moment of inertia is a fundamental concept in rotational dynamics. It quantifies an object’s resistance to changes in its rotational motion and depends on both the mass of the object and the distribution of that mass relative to the axis of rotation. Consequently, in this article, we will explore the concept of moment of inertia, derive its mathematical expressions for common shapes, and discuss important theorems like the Parallel Axis Theorem and the Perpendicular Axis Theorem.

Contents

What is Moment of Inertia?

The moment of inertia ( $I$ ) is a measure of an object’s resistance to changes in its rotational motion. That is, it depends on the mass of the object and the distribution of that mass relative to the axis of rotation. Hence, farther the mass is from the axis of rotation, the greater the moment of inertia.

Mathematical Interpretation of Moment of Inertia

If a system of consists of discrete point masses, the moment of inertia is given by:

$I = \sum_{i} m_i r_i^2$

where:

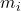$m_i$ is the mass of the 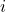$i$ -th particle,
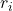$r_i$ is the perpendicular distance of the 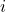$i$ -th particle from the axis of rotation.

If a system of consists a continuous mass distribution, the moment of inertia is calculated using integration:

$I = \int r^2 \, dm$

where:

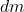$dm$ is an infinitesimal mass element,
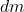$r$ is the perpendicular distance of $dm$ from the axis of rotation.

Parallel Axis Theorem of Moment of Inertia

The Parallel Axis Theorem relates the moment of inertia of an object about an axis to its moment of inertia about a parallel axis passing through its center of mass. Since most objects asymmetric about most arbitrary axes, this theorem is an extremely useful theorem. That is mathematically expressed as:

$I = I_{\text{cm}} + Md^2$

where:

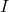$I$ is the moment of inertia about the new axis,
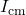$I_{\text{cm}}$ is the moment of inertia about the center of mass,
$M$ is the total mass of the object,
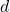$d$ is the perpendicular distance between the two axes.

Also Read: A Guide to Practical Physics

Perpendicular Axis Theorem of Moment of Inertia

The Perpendicular Axis Theorem applies to planar (2D) objects and states that the moment of inertia about an axis perpendicular to the plane of the object is the sum of the moments of inertia about two mutually perpendicular axes lying in the plane. Since most objects asymmetric about most arbitrary axes, this theorem is also an extremely useful theorem. That is expressed as:

$I_z = I_x + I_y$

where:

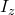$I_z$ is the moment of inertia about the perpendicular axis,
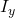$I_x$ and $I_y$ are the moments of inertia about the in-plane axes.

Moment of Inertia of Common 2D Shapes

Moment of Inertia of various shapes depends on mass, distribution of mass and the location of axis of rotation. Hence, using Symmetry, Parallel Axis Theorem and Perpendicular Axis Theorem, it can be calculated for various shapes.

Thin Rod

If one considers a thin rod of length $L$ and mass $M$ , rotating about an axis perpendicular to the rod and passing through its center, the moment of inertia can be easily calculated.

Derivation:

Firstly, divide the rod into small mass elements $dm$ of length $dx$ .

The mass per unit length is $\lambda = \frac{M}{L}$ , so $dm = \lambda dx$ .

Then the distance of each element from the center is $x$ , where $x$ ranges from $-L/2$ to $L/2$ .

Consequently, by definition, the moment of inertia is:

$I = \int_{-L/2}^{L/2} x^2 \, dm = \lambda \int_{-L/2}^{L/2} x^2 \, dx$

Then solving the integral:

$I = \lambda \left[ \frac{x^3}{3} \right]_{-L/2}^{L/2} = \lambda \left( \frac{L^3}{24} + \frac{L^3}{24} \right) = \frac{\lambda L^3}{12}$

Finally, substituting $\lambda = \frac{M}{L}$ :

$I = \frac{1}{12}ML^2$

Hence, Moment of Inertia:

$I_{\text{cm}} = \frac{1}{12}ML^2$

If the axis is at one end of the rod, using the Parallel Axis Theorem:

$I = I_{\text{cm}} + M\left(\frac{L}{2}\right)^2 = \frac{1}{12}ML^2 + \frac{1}{4}ML^2 = \frac{1}{3}ML^2$

Thin Ring

For a thin ring of mass $M$ and radius $R$ , rotating about an axis perpendicular to the plane of the ring and passing through its center.

Derivation:

Firstly, remember that all mass elements $dm$ are at a distance $R$ from the axis.

Hence, the moment of inertia is:

$I = \int R^2 \, dm = R^2 \int dm = MR^2$

Hence, Moment of Inertia:

$I = MR^2$

Solid Disc

For a solid disc of mass $M$ and radius $R$ , rotating about an axis perpendicular to the plane of the disc and passing through its center.

Derivation:

Firstly, divide the disc into thin rings of radius $r$ and thickness $dr$ .

Then the mass of each ring is $dm = \sigma \cdot 2\pi r \, dr$ , where $\sigma = \frac{M}{\pi R^2}$ is the mass per unit area.

Then, the moment of inertia of each ring is $dI = r^2 \, dm = \sigma \cdot 2\pi r^3 \, dr$ .

Integrate over the entire disc:

$I = \int_0^R \sigma \cdot 2\pi r^3 \, dr = 2\pi\sigma \int_0^R r^3 \, dr$

Then solving the integral:

$I = 2\pi\sigma \left[ \frac{r^4}{4} \right]_0^R = \frac{\pi\sigma R^4}{2}$

Finally substituting $\sigma = \frac{M}{\pi R^2}$ :

$I = \frac{1}{2}MR^2$

Hence, Moment of Inertia:

$I = \frac{1}{2}MR^2$

Rectangular Lamina

For a rectangular lamina of mass $M$ , length $a$ , and width $b$ , rotating about an axis perpendicular to the plane and passing through its center.

Derivation:

Firstly, use the Perpendicular Axis Theorem: $I_z = I_x + I_y$ .

Hence, for a thin lamina, $I_x = \frac{1}{12}Mb^2$ and $I_y = \frac{1}{12}Ma^2$ .

Thus:

$I_z = \frac{1}{12}M(a^2 + b^2)$

Hence, Moment of Inertia:

$I = \frac{1}{12}M(a^2 + b^2)$

Triangular Lamina

For a triangular lamina of mass $M$ and base $b$ , rotating about an axis perpendicular to the plane and passing through its centroid.

Derivation:

Since we know that the centroid of a triangle is located at a height $h/3$ from the base, where $h$ is the height of the triangle.

Then using calculus and integration, the moment of inertia about the centroid is:

$I = \frac{1}{36}Mb^2$

Hence, Moment of Inertia:

$I = \frac{1}{36}Mb^2$

Moment of Inertia of Common 3D Shapes

Hollow Cylinder

For a hollow cylinder of mass $M$ , inner radius $R_1$ , and outer radius $R_2$ , rotating about its central axis.

Derivation:

Firstly, note that the moment of inertia is the difference between the moments of inertia of two solid cylinders of radii $R_2$ and $R_1$ :

$I = \frac{1}{2}M_2R_2^2 - \frac{1}{2}M_1R_1^2$

Since $M = M_2 - M_1$ , and assuming uniform density:

$I = \frac{1}{2}M(R_1^2 + R_2^2)$

Hence, Moment of Inertia:

$I = \frac{1}{2}M(R_1^2 + R_2^2)$

Solid Cylinder

For a solid cylinder of mass $M$ and radius $R$ , rotating about its central axis.

Derivation:

Since we know the Moment of Inertia of a disc, using the result and integrating over the height:

$I = \frac{1}{2}MR^2$

Hence, Moment of Inertia:

$I = \frac{1}{2}MR^2$

Hollow Sphere

For a hollow sphere of mass $M$ and radius $R$ , rotating about an axis passing through its center.

Derivation:

Firstly divide the sphere into thin rings of elemental mass $dm$ .

Since surface mass density $\sigma$ is given by:

$\sigma =\frac{M}{4 \pi R^2}$

Then using spherical coordinates and integration:

$I = \frac{2}{3}MR^2$

Hence, Moment of Inertia:

$I = \frac{2}{3}MR^2$

Solid Sphere

For a solid sphere of mass $M$ and radius $R$ , rotating about an axis passing through its center.

Derivation:

Firstly divide the sphere into thin discs of elemental mass $dm$ .

Then integrate:

$I = \frac{2}{5}MR^2$

Hence, Moment of Inertia:

$I = \frac{2}{5}MR^2$

Cube

For a cube of mass $M$ and side length $a$ , rotating about an axis passing through its center and perpendicular to one of its faces.

Derivation:

Firstly, using symmetry and integration:

$I = \frac{1}{6}Ma^2$

Hence, Moment of Inertia:

$I = \frac{1}{6}Ma^2$

Table of Summation

Moment of Inertia Table — **Table 1. Summary of Derived Formulae**

Conclusion

In conclusion, moment of inertia is a fundamental concept in rotational dynamics, describing how mass is distributed relative to an axis of rotation. Thus, by understanding the mathematical derivations and applying theorems like the Parallel Axis Theorem and Perpendicular Axis Theorem, we can calculate the moment of inertia for various shapes. Therefore, these calculations are essential for analyzing the rotational motion of objects in physics and engineering.

References

Mulhayatiah, D., Suhendi, H. Y., Zakwandi, R., Dirgantara, Y., & Ramdani, M. (2018, December 4). Moment of inertia: Development of rotational dynamics KIT for physics students. IOP Conference Series: Materials Science and Engineering, 434(1), 012014. https://doi.org/10.1088/1757-899X/434/1/012014
Diaz, R., Herrera, W., & Martinez, R. (2005, August 23). Moments of inertia for solids of revolution and variational methods. European Journal of Physics, 27(2). https://doi.org/10.1088/0143-0807/27/2/001
Villamizar, D. V. (2023). Moments of inertia by summation. Revista Brasileira De Ensino De Física, 45. https://doi.org/10.1590/1806 -9126-rbef-2023-0277
Fäldt, Å., & Fredlund, T. (2023). The gyroscopic effect and moment of inertia. Physics Education, 58(2), 025001. https://doi.org/10.1088/1361-6552/aca73a

Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.

Author
Latest Posts

Uddhav Thakore

Moment of Inertia: Formulae for Different Shapes

What is Moment of Inertia?

Mathematical Interpretation of Moment of Inertia

Parallel Axis Theorem of Moment of Inertia

Perpendicular Axis Theorem of Moment of Inertia

Moment of Inertia of Common 2D Shapes

Thin Rod

Derivation:

Hence, Moment of Inertia:

Thin Ring

Derivation:

Hence, Moment of Inertia:

Solid Disc

Derivation:

Hence, Moment of Inertia:

Rectangular Lamina

Derivation:

Hence, Moment of Inertia:

Triangular Lamina

Derivation:

Hence, Moment of Inertia:

Moment of Inertia of Common 3D Shapes

Hollow Cylinder

Derivation:

Hence, Moment of Inertia:

Solid Cylinder

Derivation:

Hence, Moment of Inertia:

Hollow Sphere

Derivation:

Hence, Moment of Inertia:

Solid Sphere

Derivation:

Hence, Moment of Inertia:

Cube

Derivation:

Hence, Moment of Inertia:

Table of Summation

Conclusion

References

Top Posts

AgentKit: Simplifying Smart Agent Creation for Future STEM Innovators

Groundbreaking Quantum Discoveries Earn 2025 Nobel Prize in Physics

How Black Holes Spread Missing Ordinary Matter Across the Universe

Leave Your Comment Cancel Reply