The Puzzle Time Challenge

ANSWERS TO PUZZLE OF ISSUE 2, NOVEMBER 2023

The Puzzle Time Challenge is an incredibly exciting feature in our magazine issue. Not only is it designed to engage readers. It also offers a variety of stimulating puzzles that thoroughly test their logical reasoning and mathematical skills. Moreover, this section includes a diverse range of challenges, spanning from age-old mathematical riddles to modern problem-solving scenarios. In addition to being intellectually engaging, it provides a fun and educational experience that appeals to enthusiasts of all ages. Therefore, we encourage you to dive in, explore the solutions, and further enhance your analytical abilities in an enjoyable and rewarding way!

• Riya’s income is 20% more than his brother Rahul. How much percent is Rahul’s income less than Riya?
  Riya’s income = 20% more than Rahul’s income
  Let’s take Rahul’s income = ₹100
  Riya’s income = ₹120
  Percentage required = (20/120) × 100% = 16.67%
  Therefore, Rahul’s income is 16.67% less than Riya’s income.
• The H.C.F. and L.C.M. of two numbers are 11 and 385 respectively. If one number lies between 75 and 125, find another number.
  Product of numbers = 11 × 385 = 4235
  Let numbers be 11a and 11b.
  Then, 11a × 11b = 4235
  ⇒ ab = 35
  Now, co-primes with product 35 are (1, 35) and (5,7).
  So, numbers are (11 × 1, 11 × 35) and (11 × 5, 11 × 7)
  Since one number lies 75 and 125, suitable pair is (55,77).
  Hence, required number = 77
• By selling 110 mangoes, CP of 120 mangoes is realized. What is the gain percentage?
  Let CP of 1 mango = ₹1
  CP of 110 mangoes = ₹110
  SP of 110 mangoes = CP of 120 mangoes = ₹120
  Gain ₹120 − ₹110 = ₹10
  Thus, Gain % = Gain/CP × 100% = 10/110 × 100%
• A lamp post has half of its length in mud, 33.33 % of its length in water and 3.33 m above the water. Find the total length of the post.
  Let the length of the lamp post = x
  Length in mud = x/2
  Length of water = x/3
  Total length x = x/2 + x/3 + 10/3
  ⇒ 6x = 3x + 2x + 20
  ⇒ x = 20. The whole length of the post is 20 m.
• The sum of the square of two numbers is 146 and the square root of one of them is √5. Find the cube of the other number.

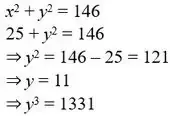
• A completes a work in 12 days. B completes the same work in 15 days. A started working alone and after 3 days B joined him. How many days will they now take together to complete the remaining work?
  Work Rate = W/(Days/Time)
  Let us assume n be the number of extra days.
  For A = W/12
  For B = W/15
  So, W/12 × (3 + n) + W/15 × (n) = W
  ⇒ (3 + n)/12 + n /15 = 1
  ⇒ n = 5
• The present age of a father is twice that of his son. 15 years ago, the age of father was thrice that of his son. What is the present age of father (in years)?
  Let the present age of the father be x and the present age of the son be y.
  So, x = 2y …. (i)
  15 years ago, father’s age was (x – 15) yeas and son’s
  age was (y – 15) years.
  According to question,
  (x – 15) = 3(y – 15) …. (ii)
  On solving equation (i) and (ii) we get:
  y = 30 and x = 15.
  Thus, father’s present age is 60 years.
• A student got 45% marks in an exam and failed by 10 marks. If the maximum marks in the exam are 200, what is the minimum percentage marks required for passing the exam?
  First, we need to find out how many marks the student got.
  Since he got 45% of the total marks, he got 45/100 ×200 = 90 marks
  He failed by 10 marks, which means the passing marks are 90 + 10 = 100
  Passing marks in percentage = 100/200 × 100% = 50%
• The denominator of a fraction is 1 more than its numerator. If 1 is deducted from both the numerator and the denominator, the fraction becomes equivalent to 0.5.
  Find the fraction.
  Let the numerator and the denominator of the fraction be x and y.
  According to question,
  y = x + 1 …. (i)
  (x – 1)/(y – 1) = 0.5 ….(ii)
  On solving equation (i) and (ii), we get:
  x = 2 and y = 3
  Thus, required fraction = 2/3
• If the diagonal of a square is equal to the diameter of a circle, then what is the ratio between the area of the square to the area of the circle?
  Let ‘a’ and ‘r’ and be side of the square and the radius of the circle respectively. Then
  Diagonal of square = a√2
  Diameter of circle = 2r
  Diagonal of square = Diameter of circle
  a√2 = 2r
  a = 2r/√2
  or a = r√2
  Now,
  Area of Square/Area of Circle = (r√2)2/ πr2 = 2/π
  Therefore, required ratio = 2: π

Puzzle Time Challenge – LET’S SOLVE IT!

The Puzzle Time Challenge is not only about finding answers but also about thoroughly understanding the underlying logic while enhancing your approach to problem-solving. Moreover, each puzzle is meticulously designed to encourage critical thinking, promote step-by-step analysis, and inspire creative solutions. By actively engaging with these challenges, readers can gradually build their mathematical intuition and learn to effectively apply concepts in real-world scenarios. Furthermore, they can enjoy the thrill of exploring complex problems presented in the Puzzle Time Challenge DECEMBER 2023 issue. Ultimately, it’s a highly rewarding experience for learners at all levels, as it offers both significant educational value and stimulating mental exercises.

1. Jack correctly remembers that his mother’s birthday is before 23rd April but after 19th April, whereas his sister correctly remembers that their mother’s birthday is
   not on or after 22nd April. On which day in April is their mother’s birthday?
2. In the following question, all the equations except one have been solved according to a certain rule. You are required to solve the unsolved equation following the same rule and to choose the correct answer out of the given options:
   4 × 6 × 2 = 351, 3 × 9 × 8 = 287, 9 × 5 × 6 =?
3. In open ground, Ron walks 20 m towards North, turns left and goes 40 m. He turns to his left again to walk 50 m. How far is he from the starting point?
4. When 6 boys were admitted & 6 girls left the percentage of boys increased from 60% to 75%. Find the original no. of boy and girl in the class.
5. The population of the village is 5000. If in a year, the number of males were to
   increase by 5% and that of a female by 3% annually, the population would grow to
   5202 at the end of the year. Find the number of males and females in the village.
6. A lotus is 2m above the water in a pond. Due to wind the lotus slides on the side and only the stem completely submerges in the water at a distance of 10m from the original position. Find the depth of water in the pond.
7. A teacher attempting to arrange the students for a mass drill in the form of a
   solid square found that 24 students were left over. When he increased the size of the square by one student, he found he was short of 25 students. Find the number of students.
8. If the minute hand of a big clock is 1.05 m long, find the rate at which its tip moves in cm per minute.
9. Find the area of the shaded region, if the side of a square is 28cm. The radius of the sector is ½ the length of the side of the square.
10. A golf ball has a diameter equal to 4.1cm. Its surface has 150 dimples each radius of 2mm. Calculate the total surface area exposed to the surroundings assuming that the dimples are hemispherical.

The Puzzle Time Challenge is much more than just a simple test of knowledge; rather, it is an enjoyable. It is an engaging way to learn, grow, and significantly enhance your logical reasoning skills. By actively tackling these puzzles, readers can not only discover creative solutions but also experience the joy and satisfaction of solving complex problems. Additionally, this feature encourages deeper engagement with challenging concepts, making learning both effective and fun. Therefore, we invite you to stay tuned for the next issue. where we will introduce even more exciting Puzzle Time challenges designed to stimulate your mind and continually push your boundaries!

Answers will be published in the January 2024 (next) issue.

Books By Jaya Ghosh

• Author
• Latest Posts

jaya-ghosh

• THE PUZZLE TIME CHALLENGE: LET'S SOLVE IT!
• The Puzzle Time Challenge
• Exam Corner - JEE MAIN 2024