The Work Energy Theorem: A Comprehensive Breakdown

Published on: March 25, 2025in

Understand the basics of work, power, and energy: conservation laws, applications, and example problems

Estimated reading time: 9 minutes

Understanding the concepts of work and energy is fundamental to the study of physics. The Work-Energy Theorem establishes a crucial relationship between the work done on an object and its change in kinetic energy. This theorem helps explain energy transformation in various real-world scenarios, such as the motion of vehicles, free-falling objects, and the operation of mechanical systems. Therefore, by delving into the Work-Energy Theorem, we gain valuable insights into the conservation and dissipation of energy.

Contents

Definition of Work and Energy

Work in Physics

Work is defined as the product of force and displacement in the direction of the force. Hence, it is expressed mathematically as:

$W = F d \cos\theta$

where:

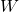$W$ is the work done (in joules, J),
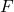$F$ is the applied force (in newtons, N),
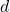$d$ is the displacement (in meters, m),
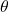$\theta$ is the angle between the force and displacement.

Work is positive when force and displacement are in the same direction and negative when they are in opposite directions. If the force is perpendicular to displacement, no work is done.

Energy

Energy is the ability of an object to do work. The two primary forms of energy in mechanics are:

Kinetic Energy (KE): The energy an object possesses due to its motion: $KE = \frac{1}{2} m v^2$
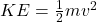
Potential Energy (PE): The stored energy due to an object’s position or configuration: $PE = mgh$

The SI unit for both work and energy is the joule (J).

The Work-Energy Theorem

Statement of the Work-Energy Theorem

The Work-Energy Theorem states that the total work done by all forces acting on an object is equal to the change in its kinetic energy:

$W = \Delta KE = KE_f - KE_i$

Hence, this theorem highlights how work influences an object’s motion.

Conceptual Understanding

If work is done in favor of an object’s motion, its kinetic energy increases. If work is done against its motion, the kinetic energy decreases. Additionally, this principle applies to vehicles slowing down, projectiles in motion, and objects moving against frictional forces.

Mathematical Derivation of the Work-Energy Theorem

Derivation Using Newton’s Second Law

Firstly, Newton’s Second Law states:

$F = ma$

Then, multiplying both sides by displacement $d$ :

$F d = ma d$

Finally, using the kinematic equation $v^2 = u^2 + 2aS$ , we derive:

$W = \frac{1}{2} m v^2 - \frac{1}{2} m u^2$

Hence, confirming that work results in a change in kinetic energy.

Integral Form of Work-Energy Theorem

For variable forces, work calculated using integration:

$W = \int_{x_1}^{x_2} F dx$

This applies to systems where force changes over distance, such as springs or resistive forces.

Applications of the Work-Energy Theorem

Motion of a Free-Falling Object

Gravity does work on a falling object. Hence, converting potential energy into kinetic energy.

Braking of a Vehicle

Moving vehicles dissipate energy as heat when brakes apply force against motion.

Work Done in Circular Motion

In vertical loops, energy transformation occurs between kinetic and potential energy.

Work-Energy in Sports and Daily Life

Since consumption of energy is common in sports, examples include running, jumping, and throwing objects, where kinetic and potential energy interact.

Types of Work and Energy

Positive, Negative, and Zero Work

Positive Work: Force and displacement in the same direction (e.g., lifting a box).
Negative Work: Force opposes displacement (e.g., friction slowing down an object).
Zero Work: Force is perpendicular to displacement (e.g., centripetal force in circular motion).

**Fig 1. In Circular Motion, no work is done as force is perpendicular to displacement**

Conservative and Non-Conservative Work

Conservative Forces: Gravity and elastic forces conserve mechanical energy.
Non-Conservative Forces: Friction and air resistance dissipate energy as heat.

Conservative Force — **Fig 2. Gravity: An example of conservative force**

Work Done by a Variable Force

Force-Displacement Graph

The area under a force-displacement graph represents the work done.

Spring Force and Work Done

For a spring obeying Hooke’s Law:

$W = \frac{1}{2} k x^2$

where $k$ is the spring constant and $x$ is the displacement from equilibrium.

spring work — **Fig 3. Hooke’s Law: Work done by a spring**

Power and Its Relation to Work

Definition of Power

The rate of work done is Power:

$P = \frac{W}{t}$

Instantaneous Power

Since power is the rate of doing work, it can be expressed as a product of Force and Velocity. Hence, for a moving object:

$P = F v$

where $v$ is velocity.

Conservative and Non-Conservative Forces

Work Done by Conservative Forces

Forces like gravity and springs store energy and allow energy recovery.

Work Done by Non-Conservative Forces

Forces like friction dissipate energy, reducing mechanical energy.

Energy Conservation and Dissipation

Law of Conservation of Mechanical Energy

Total mechanical energy remains constant when only conservative forces act:

$KE + PE = \text{constant}$

Energy Dissipation in Non-Conservative Systems

Friction and air resistance convert mechanical energy into heat. Consequently, this leads to energy loss.

Example Problems and Solutions on Work, Energy and Power

1) Work Done by a Constant Force

Problem:

A 10 kg box is pushed with a force of 50 N over a distance of 5 m on a frictionless surface. If the force is applied at an angle of 30° to the horizontal, calculate the work done by the force.

Solution:

Firstly, the work done by a force is given by:

$W = F d \cos\theta$

Then, substituting the values:

$W = (50)(5) \cos(30^\circ)$

$W = 50 \times 5 \times 0.866$

$W = 216.5 \text{ J}$

Therefore, Answer: 216.5 J

2) Conservation of Energy in a Pendulum

Work energy conservation in Pendulum — **Fig 4. Energy conserved in Pendulum**

Problem:

If a pendulum bob of mass 2 kg is raised to a height of 0.5 m, find its speed at the lowest point.

Solution:

Firstly, using conservation of mechanical energy:

$mgh = \frac{1}{2} m v^2$

Then, cancel $m$ :

$9.8(0.5) = \frac{1}{2} v^2$

$4.9 = \frac{1}{2} v^2$

$v^2 = 9.8$

$v = 3.13 \text{ m/s}$

Therefore, Answer: 3.13 m/s

3) Braking Force and Stopping Distance

Problem:

A car of mass 1000 kg is moving at 20 m/s. If the brakes apply a constant force of 5000 N to stop the car, find the stopping distance.

Solution:

Since, the work-energy theorem states:

$W = \Delta KE$

$F d = \frac{1}{2} m v^2$

$5000 d = \frac{1}{2} (1000)(20)^2$

$5000 d = 200000$

$d = 40 \text{ m}$

Therefore, Answer: 40 m

4) Work Done by a Spring

Problem:

If a spring with a force constant $k = 200$ N/m is compressed by 0.1 m. Then, calculate the work done to compress the spring.

Solution:

Since, work done on a spring:

$W = \frac{1}{2} k x^2$

$W = \frac{1}{2} (200) (0.1)^2$

$W = 1 \text{ J}$

Therefore, Answer: 1 J

5) Power in Lifting an Object

Problem:

If a crane lifts a 500 kg load to a height of 20 m in 10 seconds, find the power required.

Solution:

Since power is:

$P = \frac{W}{t}$

Hence, work done against gravity:

$W = mgh = (500)(9.8)(20) = 98000 \text{ J}$

$P = \frac{98000}{10} = 9800 \text{ W}$

Therefore, Answer: 9800 W or 9.8 kW

6) Work-Energy Theorem Applied to a Moving Car

Problem:

If a car of mass 1200 kg increases its speed from 10 m/s to 30 m/s, find the work required.

Solution:

Since:

$W = \Delta KE = \frac{1}{2} m v_f^2 - \frac{1}{2} m v_i^2$

$W = \frac{1}{2} (1200) (30^2 - 10^2)$

$W = 600 (900 - 100)$

$W = 600 \times 800 = 480000 \text{ J}$

Therefore, Answer: 480 kJ

7) Work Done in an Inclined Plane Scenario

Problem:

If a 50 kg box is pulled up a smooth incline of length 5 m and height 3 m, find the work done by the pulling force.

Solution:

We know that, work required is equal to the gain in potential energy:

$W = mgh$

$W = (50)(9.8)(3)$

$W = 1470 \text{ J}$

Therefore, Answer: 1470 J

8)Work Done by a Non-Conservative Force (Friction)

Problem:

If a 10 kg object is pushed 4 m across a rough surface with friction force 5 N, find the work done by friction.

Solution:

$W = F d \cos 180^\circ$

$W = (5)(4)(-1)$

$W = -20 \text{ J}$

Therefore, Answer: -20 J (negative work)

Frequently Asked Questions (FAQ’s)

1. Why is the Work-Energy Theorem important?

Work Energy Theorem is a fundamental interpretation of the laws of classical mechanics. Therefore, it provides a direct relationship between force, motion, and energy transfer without needing to analyze forces individually at every moment.

2. Can work be negative?

Yes, work is negative when force acts opposite to displacement, removing energy from the system.

3. How does friction affect energy conservation?

Since friction dissipates mechanical energy as heat, it reduces the total usable energy in a system.

4. Is work a scalar or vector quantity?

Work is a scalar quantity, though calculated using vector quantities (force and displacement).

5. What happens if no work is done on an object?

If no net work is done, the object’s kinetic energy remains constant.

Conclusion

In conclusion, Work, Energy and Power are fundamental concepts of physics. Since these concepts play a pivotal role in understanding every aspect of life ranging from the smallest waves to the largest bodies, they are considered the building blocks of Classical Mechanics.

References

Landau, L. D., & Lifshitz, E. M. (1986). Theory of elasticity. Pergamon Press. https://doi.org/10.1016/C2009-0-25521-8
Goldstein, H., Poole, C., & Safko, J. (2001). Classical mechanics. Addison-Wesley. https://doi.org/10.1119/1.1484149
Mínguez, J. (2005). The work–energy theorem and the first law of thermodynamics. International Journal of Mechanical Engineering Education, 33(1). https://doi.org/10.7227/IJMEE.33.1.8

Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.

Author
Latest Posts

Uddhav Thakore

The Work Energy Theorem: A Comprehensive Breakdown

Definition of Work and Energy

Work in Physics

Energy

The Work-Energy Theorem

Statement of the Work-Energy Theorem

Conceptual Understanding

Mathematical Derivation of the Work-Energy Theorem

Derivation Using Newton’s Second Law

Integral Form of Work-Energy Theorem

Applications of the Work-Energy Theorem

Motion of a Free-Falling Object

Braking of a Vehicle

Work Done in Circular Motion

Work-Energy in Sports and Daily Life

Types of Work and Energy

Positive, Negative, and Zero Work

Conservative and Non-Conservative Work

Work Done by a Variable Force

Force-Displacement Graph

Spring Force and Work Done

Power and Its Relation to Work

Definition of Power

Instantaneous Power

Conservative and Non-Conservative Forces

Work Done by Conservative Forces

Work Done by Non-Conservative Forces

Energy Conservation and Dissipation

Law of Conservation of Mechanical Energy

Energy Dissipation in Non-Conservative Systems

Example Problems and Solutions on Work, Energy and Power

1) Work Done by a Constant Force

Problem:

Solution:

2) Conservation of Energy in a Pendulum

Problem:

Solution:

3) Braking Force and Stopping Distance

Problem:

Solution:

4) Work Done by a Spring

Problem:

Solution:

5) Power in Lifting an Object

Problem:

Solution:

6) Work-Energy Theorem Applied to a Moving Car

Problem:

Solution:

7) Work Done in an Inclined Plane Scenario

Problem:

Solution:

8)Work Done by a Non-Conservative Force (Friction)

Problem:

Solution:

Frequently Asked Questions (FAQ’s)

1. Why is the Work-Energy Theorem important?

2. Can work be negative?

3. How does friction affect energy conservation?

4. Is work a scalar or vector quantity?

5. What happens if no work is done on an object?

Conclusion

References

Top Posts

AgentKit: Simplifying Smart Agent Creation for Future STEM Innovators

Groundbreaking Quantum Discoveries Earn 2025 Nobel Prize in Physics

How Black Holes Spread Missing Ordinary Matter Across the Universe

Leave Your Comment Cancel Reply