Two-Dimensional Kinematics: Motion in a Plane with Example Problems

Published on: March 6, 2025in

Understanding two dimensional kinematics and projectile motion in a plane.

Estimated reading time: 8 minutes

Kinematics is the study of motion without considering the forces causing it. While one-dimensional motion is relatively simple, most real-world motion occurs in two or three dimensions. Therefore, understanding two-dimensional kinematics is crucial for analyzing the motion of projectiles, vehicles, aircraft, and even celestial bodies.

Contents

In short, this article will explore motion in a plane, projectile motion, relative velocity in two dimensions, and uniform circular motion to develop a comprehensive understanding of two-dimensional kinematics.

Difference Between One-Dimensional and Two-Dimensional Motion

Feature	One-Dimensional Motion	Two-Dimensional Motion
Path of Motion	Straight line	Curved or angular path
Components	Only one (x or y)	Two (x and y)
Examples	A car moving on a straight road	A projectile in flight

Applications of Two-Dimensional Kinematics in Real Life

Projectile motion: For example, the motion of a soccer ball, basketball, or javelin in flight.
Navigation: Ships and aircraft move in two dimensions, because they require precise calculations.
Sports physics: Specifically, analyzing the curved trajectory of a golf ball or a baseball pitch.
Space exploration: The motion of both satellites and planetary orbits follows two-dimensional kinematics principles.

Moon trajectory — **Fig 1. Orbital Trajectory of the Moon Projected into 2 Dimensions**

How to Analyze Motion in Two Dimensions?

Understanding Vectors in Two-Dimensional Motion

Since motion in two dimensions involves both horizontal and vertical components, we use vectors to represent displacement, velocity, and acceleration.

A vector has both magnitude and direction. For example, a car moving 60 km/h north has both a speed (scalar magnitude) and a direction.

Vector Components

A vector $\mathbf{A}$ in two dimensions can be broken down into:

$A_x=A\cdot \cos{\theta}$

$A_y=A\cdot \sin{\theta}$

Here, $\theta$ is the angle the vector makes with the horizontal x-axis.

Using the Pythagorean Theorem for Displacement

To find the total displacement when an object moves in two directions, we use the Pythagorean theorem:

$R=\sqrt{x^{2}+y^{2}}$

where $x$ and $y$ are the horizontal and vertical displacements.

Therefore, $x=r \cos {\theta}, y =r sin{\theta}$

Equations of Motion in Two Dimensions

Kinematic equations apply separately to x and y components in two-dimensional motion.

$v_x=u_{x}+a_{x}t$

$v_y = u_{y} + a_{y} t$

$s_x = u_{x} t + \frac{1}{2} a_{x }t^{2}$

$s_y = u_{y} t + \frac{1}{2} a_{y} t^{2}$

Since motion in the x-direction and y-direction are independent, we analyze them separately using these equations.

Projectile Motion

Definition and Characteristics

Projectile motion is specifically, a type of two-dimensional motion where an object moves under the influence of gravity alone. The horizontal velocity remains constant, while the vertical velocity changes due to acceleration from gravity.

Key Characteristics of Projectile Motion:

The only force acting on the projectile is gravity (assuming no air resistance).
Motion in the horizontal direction is uniform (constant velocity).
Motion in the vertical direction is accelerated (due to gravity $\mathbf{g}=9.8 ms^{-2}$ ).
The trajectory is parabolic, in other words, the object follows a curved path.

Components of Projectile Motion: Horizontal and Vertical

Horizontal Motion: No acceleration ( 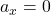$a_x = 0$ ), so velocity remains constant.
Vertical Motion: Accelerated motion ( 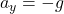$a_y = -g$ ), following the equations of motion.

Equations for Projectile Motion:

$x=ut \cos⁡{\theta}$

$y=u t\sin⁡{\theta}- \frac{1}{2}gt^{2}$

$v_y=u \sin{\theta}- gt$

Relative Motion in Two Dimensions

Definition and Concept

Relative velocity describes the velocity of one object as observed from another moving object.

If two objects A and B have velocities $\mathbf{v_A}$ and $\mathbf{v_B}$ , then the velocity of A relative to B is:

$\mathbf{v_{AB}}=\mathbf{v_A}-\mathbf{v_B}$

$\mathbf{v_{AB}}= (v_{A_x}-v_{B_x}) \mathbf{\hat{i}} + (v_{A_y} - v_{B_y})\mathbf{\hat{j}}$

Similarly, the velocity of B relative to A is:

$\mathbf{v_{AB}}=\mathbf{v_A}-\mathbf{v_B}$

$\mathbf{v_{BA}}= (v_{B_x}-v_{A_x}) \mathbf{\hat{i}} + (v_{B_y} - v_{A_y})\mathbf{\hat{j}}$

Relativity applies to Physics, not Ethics

-Albert Einstein

Examples of Relative Motion in Two Dimensions:

A boat crossing a river with a current.
An airplane flying in the presence of wind.

**Fig 3 An example of Relative Velocity in 2 Dimensions as experienced by 2 Boats**

Uniform Circular Motion

Definition and Characteristics

Uniform circular motion occurs when an object moves along a circular path with constant speed but changing direction. Therefore, this is a type of two-dimensional kinematics.

The velocity of the object is tangential to the circular path, and consequently, the acceleration (centripetal acceleration) always points toward the center of the circle.

It’s not foreign for me to be talking about my problems in circles.
-Mathew Perry

Equations for Uniform Circular Motion

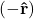Centripetal acceleration: $a_c=\frac{v^{2}}{r}\mathbf{(-\hat{r})}$ where $v$ is the speed and $r$ is the radius of the circular path. $\mathbf{(-\hat{r})}$ indicates radially inward direction.
Centripetal force: $\mathbf{F_c}=\frac{m v^{2}}{r} \mathbf{(-\hat{r})}$

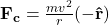
For Example:

Motion of a satellite around Earth.
A car turning in a circular track.

Uniform Circ Motion — **Fig 4. Uniform Circular Motion of Ferris Wheel**

Example Problems

Problem 1: Projectile Motion – Finding Maximum Height

Problem Statement:

In case, an American football is thrown with an initial velocity of 25 m/s at an angle of 40° above the horizontal. Then, calculate the maximum height reached by the ball.

Solution:

The maximum height is reached when the vertical velocity becomes zero.

Given:

Initial velocity $\mathbf{u} = 25 ms^{-1}$
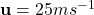
Angle $\theta = 40^{o}$
Acceleration due to gravity $\mathbf{g} = 9.8 m s^{-2}$

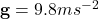
Step 1: Find the Initial Vertical Velocity

Since, the vertical component of velocity is:
$u_y = |\mathbf{u}| \sin{\theta}= 25 \sin{ 40^{o}}$
$u_y = \mathbf{16.07 ms^{-1}}$

Step 2: Use the Kinematic Equation for Projectile Motion

Then, using the equation: $v_{y}^{2} = u_{y}^{2} - 2 g h_{max}$

At maximum height, $v_y = 0$ , so:
$0 = (16.07)^{2} - 2*(9.8) h_{max}$
Solving for $h_{max}$ :
$h_{max }= \frac{16.07^{2}}{2 * 9.8} = \mathbf{13.2 m}$

Answer: Hence, the maximum height is 13.2 m.

Problem 2: Relative Velocity – Boat Crossing a River

Problem Statement:

Initially, a boat is trying to cross a 200-meter-wide river flowing at 4 m/s. The boat’s speed in still water is 10 m/s. If the boat is pointed straight across the river, determine:
a) The time taken to cross.
b) The boat’s actual velocity.

Solution:

Step 1: Time to Cross the River

Since the boat moves straight across, its effective velocity in the perpendicular (y) direction is:
$u_y = 10 m/s$

Since, time taken:
t = Width of River / Boat’s Speed in y-direction
t = 200 / 10 = 20 s

Step 2: Find the Actual Velocity of the Boat

Because the boat’s motion is in two dimensions, it has two velocity components:

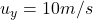$u_y = 10 m/s$ (across the river)
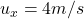$u_x = 4 m/s$ (due to river current)

Then, using the Pythagorean theorem:

$u_{actual }= \sqrt{(u_{x}^{2} + u_{y}^{2})} = \sqrt{4^{2} + 10^{2}}= \sqrt{116} = \mathbf{10.77 m/s}$

Answer: Hence,

(a) The boat takes 20 s to cross the river.
(b) The actual velocity of the boat is 10.77 m/s.

Problem 3: Uniform Circular Motion – Finding Centripetal Force

Problem Statement:

Given that, a 1,000 kg car is moving along a circular track of 50 m radius at a speed of 20 m/s. Then, calculate the centripetal force acting on the car.

Solution:

Since, the formula for centripetal force is:

$|\mathbf{F_c}| = \frac{m u^{2}}{ |\mathbf{r}|}$

Thereafter, substituting values:

$|F_c| = \frac{1000 \cdot 20^{2}}{ 50}$

$\mathbf{F_c} = 400000 / 50 = 8000 N (\mathbf {-\hat{r}})$

Answer: Hence, the centripetal force acting radially inward on the car is 8000 N.

Problem 4: Projectile Motion – Finding the Range of a Projectile

Problem Statement:

Initially, a projectile is launched at 30 m/s at an angle of 50°. Then, find the horizontal range of the projectile.

Solution:

Since, the formula for range in projectile motion is:

$|\mathbf{R}| = \frac{u^{2}\cdot \sin {2\theta}}{g}$

Thereafter, substituting values:
$R = \frac{(900 \sin{100^{o}})}{9.8} = \frac{(900 *0.9848)}{9.8}$

$\mathbf{R} = 90.43 \text{ m }( \mathbf{\hat{i}})$

Answer: Hence, the range of the projectile is 90.43 m in the x-direction.

Problem 5: Two-Dimensional Motion – Finding Final Velocity

Problem Statement:

Given that, a ball is thrown with an initial velocity of 15 m/s at an angle of 37°. Then, find the speed of the ball after 2 seconds.

Solution:

Step 1: Break Velocity into Components

Initial velocity components:
$u_x = 15\cdot \cos{37^{o}} = 15 * 0.7986 = 11.98 m/s$
$u_y = 15 \cdot \sin{37^{o}} = 15 * 0.6018 = 9.03 m/s$

Step 2: Find Vertical Velocity After 2 Seconds

Then, using the equation $v_y = u_{y} + a \cdot t$ :
$v_y = 9.03 - (9.8 * 2)$
$v_y = -10.57 m/s$

Step 3: Find the Final Speed

Thereafter, using the Pythagorean theorem:
$|\mathbf{v}| = \sqrt{u_{x}^{2} + v_{y}^{2}}$
$|\mathbf{v}| = \sqrt{11.98^{2} + (-10.57)^{2}}$

$|\mathbf{v}| =15.98 m/s$

Answer: Hence, the speed of the ball after 2 seconds is 15.98 m/s.

Conclusion

Hence, we have learnt that two-dimensional kinematics is crucial for understanding real-world motion, from projectile problems to relative motion and circular motion. Therefore, by breaking motion into vector components and applying kinematic equations separately to horizontal and vertical directions, we can analyze and solve motion problems effectively.

References

Kamberaj, H. (2021). Two- and three-dimensional motion. In Classical mechanics (pp. 55–76). De Gruyter. https://doi.org/10.1515/9783110755824-004
Gea-Banacloche, J. (2017). University physics I: Classical mechanics. University of Arkansas Open Educational Resources. https://doi.org/10.54119/NDLA8675
Flores-Garduno, E., Mancas, S. C., Rosu, H. C., & Perez-Maldonado, M. (2020). Planar motion with Fresnel integrals as components of the velocity. arXiv preprint arXiv:2005.09060. https://doi.org/10.48550/arXiv.2005.09060
Khorrami, M., Aghamohammadi, A., & Aghamohammadi, C. (2023). Slipping and rolling on a rough accelerating surface. arXiv preprint arXiv:2307.15836. https://doi.org/10.48550/arXiv.2307.15836
Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics Extended (10th ed.). John Wiley & Sons.
Serway, R. A., & Jewett, J. W. (2014). Physics for Scientists and Engineers with Modern Physics (9th ed.). Cengage Learning.

Additionally, to stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics. Further, at ENTECH Online, you’ll find a wealth of information.

Author
Latest Posts

Uddhav Thakore

Uddhav Thakore is a passionate Physicist with a Master’s degree, specializing in Astrophysics and Quantum Physics. With expertise in Mechanics, Wave Theory, the Standard Model, Engineering Electronics, and Control Systems, Uddhav is dedicated to making complex scientific concepts clear and engaging for a broad audience.

Two-Dimensional Kinematics: Motion in a Plane with Example Problems

Difference Between One-Dimensional and Two-Dimensional Motion

Applications of Two-Dimensional Kinematics in Real Life

How to Analyze Motion in Two Dimensions?

Understanding Vectors in Two-Dimensional Motion

Vector Components

Using the Pythagorean Theorem for Displacement

Equations of Motion in Two Dimensions

Projectile Motion

Definition and Characteristics

Components of Projectile Motion: Horizontal and Vertical

Relative Motion in Two Dimensions

Definition and Concept

Uniform Circular Motion

Definition and Characteristics

Equations for Uniform Circular Motion

Example Problems

Problem 1: Projectile Motion – Finding Maximum Height

Problem Statement:

Solution:

Step 1: Find the Initial Vertical Velocity

Step 2: Use the Kinematic Equation for Projectile Motion

Problem 2: Relative Velocity – Boat Crossing a River

Problem Statement:

Solution:

Step 1: Time to Cross the River

Step 2: Find the Actual Velocity of the Boat

Problem 3: Uniform Circular Motion – Finding Centripetal Force

Problem Statement:

Solution:

Problem 4: Projectile Motion – Finding the Range of a Projectile

Problem Statement:

Solution:

Problem 5: Two-Dimensional Motion – Finding Final Velocity

Problem Statement:

Solution:

Step 1: Break Velocity into Components

Step 2: Find Vertical Velocity After 2 Seconds

Step 3: Find the Final Speed

Conclusion

References

Top Posts

Body Fluids and Circulation: Key Concepts of the Circulatory System

Exercise Boosts Heart Health and Longevity

RAD@home: Rare Cosmic Radio Rings Expanding Universe Views

Leave Your Comment Cancel Reply