Mathematics is a field that has been studied and developed for thousands of years. Its origins can be traced back to ancient civilizations such as the Egyptians, Babylonians, and Greeks. These early civilizations used mathematics for practical purposes such as measuring land, building structures, and predicting astronomical events. Over time, mathematics evolved into a more abstract and theoretical discipline, with mathematicians exploring concepts such as numbers, shapes, and patterns. Many of the high school students often struggles to understand the evolution and use of the mathematics. This blog presents a concise introduction to mathematics to spark interest of high school students in the subject. The importance of mathematics in everyday life cannot be overstated. It is a fundamental tool that we use to make sense of the world around us. From calculating the cost of groceries to understanding the laws of physics, mathematics is involved in almost every aspect of our daily lives. It helps us solve problems, make decisions, and think critically. Without mathematics, our modern world would not be possible.
Key Takeaways
- Mathematics is a fundamental subject that involves the study of numbers, quantities, and shapes.
- Algebra is the language of mathematics and involves the use of symbols and equations to solve problems.
- Geometry is the study of shapes and their properties, including angles, lines, and curves.
- Calculus is the branch of mathematics that deals with the study of change and rates of change.
- Trigonometry is the study of triangles and their properties, including angles, sides, and relationships between them.
Algebra: The Language of Mathematics
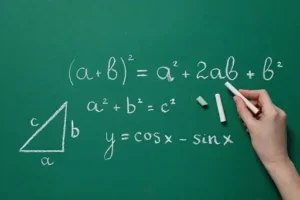Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols. It is often referred to as the language of mathematics because it allows us to express relationships between quantities and solve problems using equations and inequalities. In algebra, we use symbols such as x and y to represent unknown quantities, and we use operations such as addition, subtraction, multiplication, and division to manipulate these symbols. By using these operations, we can solve equations and inequalities to find the values of the unknowns. Solving equations and inequalities is an essential skill in algebra. Equations are mathematical statements that assert the equality of two expressions, while inequalities assert that one expression is greater than or less than another. By solving equations and inequalities, we can find solutions that satisfy the given conditions.
Geometry: The Study of Shapes
Geometry is a branch of mathematics that deals with the properties and relationships of shapes. It is derived from the Greek words “geo” meaning earth and “metron” meaning measure. Geometry has been studied for thousands of years and has applications in various fields such as architecture, engineering, and art. In geometry, we study different types of shapes such as points, lines, angles, triangles, circles, and polygons. Each shape has its own unique properties and characteristics. For example, a triangle has three sides and three angles, while a circle has a curved boundary and is defined by its radius and diameter. The applications of geometry in real life are vast. Architects use geometry to design buildings and structures that are aesthetically pleasing and structurally sound. Engineers use geometry to calculate distances, angles, and areas when designing bridges, roads, and tunnels. Artists use geometry to create visually appealing compositions and sculptures. Geometry is also used in navigation, astronomy, and computer graphics.
Calculus: The Mathematics of Change
Calculus is a branch of mathematics that deals with the study of change. It is derived from the Latin word “calculus” meaning small stone or pebble, which was used by ancient mathematicians for counting and calculating. Calculus is divided into two main branches: differentiation and integration. Differentiation is the process of finding the rate at which a quantity changes with respect to another quantity. It allows us to calculate slopes of curves, velocities of moving objects, and rates of growth or decay. Integration is the process of finding the accumulation of quantities over a given interval. It allows us to calculate areas under curves, volumes of solids, and total amounts of quantities. The applications of calculus in real life are numerous. It is used in physics to describe the motion of objects, in economics to model supply and demand curves, in biology to study population growth, and in engineering to design structures that can withstand stress and strain.
Trigonometry: The Study of Triangles
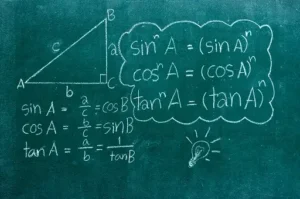Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is derived from the Greek words “trigonon” meaning triangle and “metron” meaning measure. Trigonometry is based on trigonometric functions such as sine, cosine, and tangent, which relate the angles of a triangle to the lengths of its sides. These functions are used to solve problems involving angles, distances, heights, and velocities. Trigonometry has applications in various fields such as navigation, surveying, physics, and engineering. It is used by pilots and navigators to calculate distances and directions, by surveyors to measure land and create maps, by physicists to study waves and oscillations, and by engineers to design structures that can withstand forces and vibrations.
Arithmetic: The Basics of Mathematics
Arithmetic is the most basic branch of mathematics. It deals with the properties and operations of numbers. The word “arithmetic” is derived from the Greek word “arithmos” meaning number. In arithmetic, we study the four basic operations: addition, subtraction, multiplication, and division. Addition is the process of combining two or more numbers to find their sum. Subtraction is the process of taking away one number from another to find the difference. Multiplication is the process of repeated addition, while division is the process of sharing a quantity equally. Arithmetic has applications in everyday life. We use it to count money, calculate distances and time, measure ingredients for cooking, and solve everyday problems. It is also the foundation for more advanced branches of mathematics such as algebra and calculus.
Linear Equations and Inequalities
Quadratic Equations and Functions
Quadratic equations and functions are mathematical expressions that involve quadratic terms. A quadratic equation is an equation in which the highest power of the variable is two. It can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants. Solving quadratic equations involves factoring, completing the square, or using the quadratic formula. The solutions to a quadratic equation are the values of the variable that make the equation true. Quadratic functions are mathematical expressions that involve quadratic terms. They can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. Quadratic functions have a parabolic shape and can be used to model various real-life phenomena such as projectile motion and population growth. Quadratic equations and functions have applications in various fields such as physics, engineering, and finance. They are used to model the motion of projectiles, design structures that can withstand forces and vibrations, and calculate financial investments.
The Pythagorean Theorem and Its Applications
The Pythagorean theorem is a fundamental result in geometry that relates the lengths of the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. The Pythagorean theorem can be written as a^2 + b^2 = c^2, where a and b are the lengths of the legs of the triangle, and c is the length of the hypotenuse. The Pythagorean theorem has numerous applications in real life. It is used in construction to ensure that buildings and structures are square and level. It is used in navigation to calculate distances and directions. It is used in trigonometry to derive trigonometric identities and solve trigonometric equations. Other theorems related to the Pythagorean theorem include the converse of the Pythagorean theorem, which states that if the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle.
Applications of Mathematics in Real Life
Mathematics has countless applications in various fields such as science, engineering, finance, and technology. In science, mathematics is used to describe and predict natural phenomena. In engineering, mathematics is used to design structures and solve complex problems. In finance, mathematics is used to calculate interest rates, analyze investments, and manage risk. In technology, mathematics is used to develop algorithms, analyze data, and create computer simulations. The importance of mathematics in problem-solving and decision-making cannot be overstated. It provides us with a systematic way of thinking and analyzing information. It helps us make sense of complex situations and find solutions to difficult problems. It allows us to make informed decisions based on evidence and logical reasoning. In conclusion, mathematics is a fundamental discipline that has been studied and developed for thousands of years. It is a tool that we use to understand the world around us and solve problems. From algebra to calculus, geometry to trigonometry, arithmetic to linear equations, mathematics is involved in almost every aspect of our daily lives. Its applications in various fields such as science, engineering, finance, and technology are vast and essential. Without mathematics, our modern world would not be possible. If you’re interested in exploring the fascinating world of mathematics further, you might also enjoy reading the article “How Gravity Can Be Altered” from the November 2023 issue of EnTech Online. This thought-provoking piece delves into the concept of altering gravity and its potential implications on various biological systems. It’s a captivating read that will surely expand your understanding of the fundamental forces that shape our universe. Check it out here.
FAQs
What is the article about?
The article is about providing a brief introduction to mathematics for high school students.
Why is it important for high school students to learn mathematics?
Mathematics is an essential subject that helps students develop critical thinking, problem-solving, and analytical skills. It is also a fundamental subject for many fields, including science, engineering, and finance.
What topics are covered in the article?
The article covers various topics, including algebra, geometry, trigonometry, calculus, and statistics.
What is algebra?
Algebra is a branch of mathematics that deals with mathematical symbols and the rules for manipulating these symbols to solve equations and understand mathematical relationships.
What is geometry?
Geometry is a branch of mathematics that deals with the study of shapes, sizes, positions, and properties of objects in space.
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the study of triangles and the relationships between their sides and angles.
What is calculus?
Calculus is a branch of mathematics that deals with the study of rates of change and accumulation. It is used in many fields, including physics, engineering, and economics.
What is statistics?
Statistics is a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It is used in many fields, including business, healthcare, and social sciences.
How can high school students benefit from learning mathematics?
High school students can benefit from learning mathematics in many ways, including developing critical thinking and problem-solving skills, improving their logical reasoning abilities, and preparing for college and future careers.
