Limits in Algebra: Surprising Truths
Limits in algebra help us understand what happens to a function when it approaches a certain value.
When you hear the word “limit” you might think of something that stops or restricts.
For example, roller coasters have height limits for safety. But in mathematics, limits have a different meaning.
A limit is the value a function approaches as its input gets closer to some value.
This is helpful when the input comes very close to a specific number. This applies even if we can’t actually reach that number. Imagine you’re running a race, and you see the finish line. As you run, you get closer to the finish line, but you might never actually cross it. In algebra, limits describe this idea.
For example, let’s say we have a function like f(x) = 2x. We want to find the limit of this function as x approaches 3. We look at the values of f(x) when x is really close to 3, like 2.9 or 3.1.
As x gets closer to 3, f(x) gets closer to 6. So, the limit of f(x) as x approaches 3 is 6.
This concept is essential in calculus. It helps us understand how functions behave near specific points.
There are several ways to find limits. These include direct substitution, factoring, rationalization, and using standard results.
For example, consider the function f(x) = (x2 - 4)/(x - 2). We can find the limit as x approaches 2 by factoring the numerator.
We get f(x) = (x + 2)(x - 2)/(x - 2).
As x approaches 2, the (x - 2) terms in the numerator and denominator cancel out. This leaves us with the limit of f(x) as x approaches 2 being equal to 4.
We can also use limits to find the slope of a tangent line. The tangent line touches the curve at one specific point. This concept is called the derivative. It is a fundamental concept in calculus. By understanding limits, students can build a strong foundation for more advanced topics in algebra.
Don’t worry if this sounds confusing! Let’s look at a simple example to clarify.
The Car and the Wind
Imagine two cars:
- Car 1 travels from point A to point B at a constant speed and then back from B to A at the same constant speed.
- Car 2 travels the same route with a constant wind blowing in the direction from A to B. This wind speeds Car 2 up on the way to B and slows it down on the way back to A.
Here’s the question: Will Car 2 complete its journey faster or slower than Car 1?
Intuition might suggest that Car 2 would take the same amount of time as Car 1. After all, Car 2 is faster going from A to B and slower going back from B to A, so the times might balance out.
However, this intuition is incorrect. Car 2 will always take longer than Car 1 at any given wind speed.
But How? Lets understand by applying the concept of limits.
Limits in algebra – extreme wind cases
Let’s explore extreme wind situations to understand why:
- No Wind: If there’s no wind, Car 2 travels at the same speed as Car 1, so they would finish at the same time.
- Very Strong Wind: If the wind is very strong, Car 2 will travel from A to B almost instantly. However, on the way back, Car 2 will struggle so much that Car 1 will complete the round trip before Car 2 can return.
- Wind Speed Equals Car Speed: If the wind speed is exactly the same as Car 2’s speed, Car 2 will never be able to return from B to A because the wind cancels out the car’s speed completely.
As you can see, the concept of limits can be very useful to answer such confusing questions.
If you want to play around with values and test how things turn out on different values, use this custom playground that we have built for you: https://subpixels.netlify.app/blogs/1
But to be complete and transparent lets see the proof using physics.
Proof using Algebra
Let’s use a bit of algebra to see why this happens:
- Distance between A and B: d
- Car’s speed in still air: v
- Wind speed: w
Time for Car 2 to travel from A to B:
![]()
Time for Car 2 to travel from B to A
![]()
Total Round-Trip Time for Car 2:
![]()
![]()
To combine these times, we use a common denominator:
![]()
![]()
![]()
The key point is the denominator, v2 - w2. As the wind speed w increases, the denominator gets smaller. When the wind speed equals the car’s speed (v = w), the denominator becomes zero, making the total time infinite. This matches our observation that Car 2 can’t move when the wind speed is too high.
So, as we turn up the wind, Car 2 will always take more time than Car 1, illustrating a surprising truth revealed by limits.
But there is more to this example, apart from limits or algebra, this car and wind example is often used to elaborate and draw analogy to a completely different problem in physics. More specifically, this was used in one of the most important discovery called Michelson–Morley experiment.
To learn more, check the following links:
https://www.diva-portal.org/smash/get/diva2:780834/FULLTEXT01.pdf
https://faculty.etsu.edu/gardnerr/5310/5310pdf/dg2-2.pdf
https://www.gsjournal.net/Science-Journals/Essays-Relativity%20Theory/Download/7493
https://www.hunter.cuny.edu/physics/courses/physics100/repository/spring20/Phy100sp20Lec3.pdf
Limits in algebra – One more example
Imagine a ball that is dropped from a certain height and bounces back to a fraction of the height from which it fell. Let’s say the ball bounces back to 50% of its previous height each time. The question is: How many times will the ball bounce before it effectively comes to a stop?
Our intuition might suggest that the ball will eventually come to a complete stop after a certain number of bounces. However, when we look at the problem more closely using limits, a surprising truth emerges.
Solution:
Initial Drop and Bounces:
Suppose the ball is dropped from a height say:
![]()
After the first bounce, it reaches a height:
![]()
After the second bounce, it reaches:
![]()
This pattern continues, with the height of each bounce is:
![]()
Where n is the number of bounces.
Total Distance Travelled:
To find the total distance the ball travels, we need to add the distances of all the bounces.
The distance for each bounce up and down is given by the sum of a geometric series.
Total distance D can be calculated as:
![]()
The series inside the parentheses is a geometric series where each term is 1/2 of the previous term.
Sum of the Geometric Series:
First term:
![]()
and common ratio:
![]()
Then sum S of an infinite geometric series is:
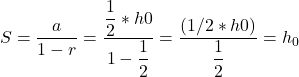
So, the total distance travelled is:
![]()
Our intuition might suggest that after a finite number of bounces, the ball will come to a stop. However, the limit shows that even though the ball bounces forever with decreasing heights, the total distance it travels converges to a finite amount, specifically three times the initial height from which it was dropped. This surprising result is a consequence of how limits help us understand infinite processes in a finite context.
Conclusion
Limits in algebra have numerous real-world applications, ranging from finance and economics to physics and engineering.
To stay updated with the latest developments in STEM research, visit ENTECH Online. This is our digital magazine for science, technology, engineering, and mathematics.
At ENTECH Online, you’ll find a wealth of information. We offer insights and resources to fuel your curiosity. Our goal is to inspire your passion for new scientific discoveries.
good one
Great article! The explanation of limits in algebra and their surprising implications was very enlightening. Thanks for breaking down these complex concepts so clearly!